Un ingénieur spécialiste des salles blanches analyse un plan de surface de réponse pour déterminer l'influence de la durée, de la température et de la pression de la thermosoudeuse sur la qualité de l'emballage stérile des plateaux. La réponse est de type binaire : l'emballage est intact ou non sur un échantillon de 800 plateaux.
L'ingénieur collecte des données et analyse le plan afin de déterminer quels facteurs ont un impact sur la résistance de la fermeture.
- Ouvrez le fichier de données échantillons, PlateauStérile.MWX.
- Sélectionnez .
- Dans la zone Nom d'événement, saisissez Evénement.
- Dans la zone Nombre d'événements, saisissez Intacts.
- Dans la zone Nombre d'essais, saisissez Echantillons.
- Cliquez sur Termes.
- Dans Inclure les termes suivants, sélectionnez Quadratique complet.
- Cliquez sur OK.
- Cliquez sur Graphiques.
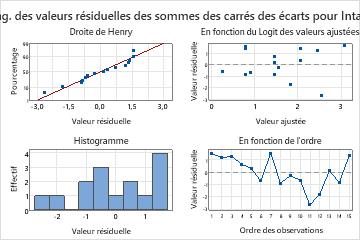
- Sous Graphiques des valeurs résiduelles, sélectionnez Quatre en un.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
Dans le tableau Analyse de la variance, les valeurs de p pour Température, Pression et Température*Température sont significatives. L'ingénieur peut envisager de réduire le modèle pour retirer les termes non significatifs. Pour plus d'informations, reportez-vous à la rubrique Réduction du modèle.
La valeur R2 de la somme des carrés d'écart indique que le modèle explique 97,47 % de la somme totale des carrés d'écart de la réponse, ce qui indique qu'il est extrêmement bien ajusté aux données.
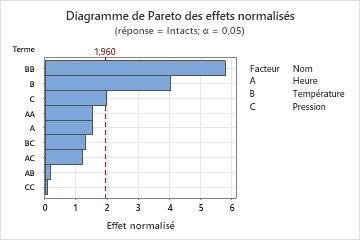
Le diagramme de Pareto vous permet de repérer visuellement les effets importants et de comparer l'importance relative des divers effets. De plus, vous voyez que l'effet le plus important est celui du terme Température*Température (BB), car c'est celui qui a la barre la plus grande.
Méthode
| Fonction de liaison | Logit |
|---|---|
| Lignes utilisées | 15 |
Informations de réponse
| Variable | Valeur | Dénombrement | Nom d'événement |
|---|---|---|---|
| Intacts | Evénement | 9637 | Evénement |
| Non-événement | 2363 | ||
| Echantillons | Total | 12000 |
Coefficients codés
| Terme | Coeff | Coef ErT | FIV |
|---|---|---|---|
| Constante | 3,021 | 0,384 | |
| Heure | 0,210 | 0,139 | 18,53 |
| Température | 0,641 | 0,159 | 19,53 |
| Pression | 0,420 | 0,211 | 70,48 |
| Heure*Heure | -0,0735 | 0,0482 | 1,01 |
| Température*Température | 0,2988 | 0,0517 | 1,17 |
| Pression*Pression | -0,0022 | 0,0277 | 70,24 |
| Heure*Température | -0,0092 | 0,0505 | 1,14 |
| Heure*Pression | 0,0417 | 0,0342 | 18,12 |
| Température*Pression | -0,0521 | 0,0396 | 19,24 |
Rapports des probabilités de succès pour les prédicteurs continus
| Incrément | Rapport des probabilités de succès | IC à 95 % | |
|---|---|---|---|
| Heure | 1,0 | * | (*; *) |
| Température | 25,0 | * | (*; *) |
| Pression | 7,5 | * | (*; *) |
Récapitulatif du modèle
| R carré de la somme des carrés des écarts | R carré (ajust) de la somme des carrés des écarts | AIC | AICc | BIC |
|---|---|---|---|---|
| 97,47% | 96,50% | 140,64 | 195,64 | 147,72 |
Tests d'adéquation de l'ajustement
| Test | DL | Khi deux | Valeur de p |
|---|---|---|---|
| Somme des carrés des écarts | 5 | 23,40 | 0,000 |
| Pearson | 5 | 23,88 | 0,000 |
| Hosmer-Lemeshow | 5 | 7,47 | 0,188 |
Analyse de la variance
| Source | DL | Somme des carrés des écarts ajustée | Moyenne ajustée | Khi deux | Valeur de p |
|---|---|---|---|---|---|
| Modèle | 9 | 903,478 | 100,386 | 903,48 | 0,000 |
| Heure | 1 | 2,303 | 2,303 | 2,30 | 0,129 |
| Température | 1 | 16,388 | 16,388 | 16,39 | 0,000 |
| Pression | 1 | 3,966 | 3,966 | 3,97 | 0,046 |
| Heure*Heure | 1 | 2,331 | 2,331 | 2,33 | 0,127 |
| Température*Température | 1 | 34,012 | 34,012 | 34,01 | 0,000 |
| Pression*Pression | 1 | 0,006 | 0,006 | 0,01 | 0,937 |
| Heure*Température | 1 | 0,033 | 0,033 | 0,03 | 0,856 |
| Heure*Pression | 1 | 1,490 | 1,490 | 1,49 | 0,222 |
| Température*Pression | 1 | 1,731 | 1,731 | 1,73 | 0,188 |
| Erreur | 5 | 23,404 | 4,681 | ||
| Total | 14 | 926,882 |
Equation de régression en unités non codées
| P(Evénement) | = | exp(Y')/(1 + exp(Y')) |
|---|
| Y' | = | 17,77 + 0,348 Heure - 0,1918 Température + 0,1146 Pression - 0,0735 Heure*Heure + 0,000478 Température*Température - 0,000039 Pression*Pression - 0,00037 Heure*Température + 0,00556 Heure*Pression - 0,000278 Température*Pression |
|---|
Ajustements et diagnostics pour les observations aberrantes
| Observation | Probabilité observée | Valeur ajustée | Résiduelle | Val. résid. norm. | |
|---|---|---|---|---|---|
| 1 | 0,7113 | 0,6856 | 1,5722 | 4,45 | R |
| 3 | 0,9025 | 0,8879 | 1,3370 | 2,50 | R |
| 7 | 0,9675 | 0,9565 | 1,5927 | 2,17 | R |
| 8 | 0,6737 | 0,6884 | -0,8891 | -2,44 | R |
| 10 | 0,5550 | 0,5660 | -0,6265 | -2,07 | R |
| 11 | 0,9025 | 0,9281 | -2,6700 | -4,20 | R |
| 12 | 0,8413 | 0,8633 | -1,7806 | -3,54 | R |
| 15 | 0,7113 | 0,6892 | 1,3592 | 3,64 | R |