Sur ce thème
Plans de mélange centrés
Un plan de mélange centré pour un mélange avec q composantes comporte 2**q – 1 points. Les points du plan sont les suivants :
- Tous les points (x1, x2, ..., xq) dont une composante, xi, est égale à 1, tandis que les autres ont pour valeur 0. Ces points sont les points des sommets.
- Tous les points dont une composante, xi, est égale à 1/2, et une autre, xj, est égale à 1/2, tandis que les autres ont pour valeur 0.
- Tous les points dont une composante, xi, est égale à 1/3, une autre composante, xj, est égale à 1/3, une autre composante, xk, est égale à 1/3, tandis que les autres ont pour valeur 0.
- Ce schéma continue jusqu'à ce que toutes les composantes soient égales à 1/q. Ce dernier point (où toutes les composantes sont égales) est appelé centre ou centré du plan.
Plans en réseaux
| Degré du maillé (m) | Nombre de composants (q) |
|---|---|
| 1 | 2 à 20 |
| 2 | 2 à 20 |
| 3 | 2 à 17 |
| 4 | 2 à 11 |
| 5 | 2 à 8 |
| 6 | 2 à 7 |
| 7 | 2 à 6 |
| 8 | 2 à 5 |
| 9 | 2 à 5 |
| 10 | 2 à 5 |
Plans sous contraintes
Minitab génère les sommets extrêmes de l'espace de plan contraint à l'aide de l'algorithme XVERT, puis calcule les points centraux jusqu'au degré spécifié à l'aide de l'algorithme CONAEV de Piepel. Pour plus d'informations, reportez-vous à Cornell1 et St. John2.
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
- R.C. St. John (1984). "Experiments With Mixtures in Conditioning and Ridge Regression," Journal of Quality Technology 16, pp.81-96.
Types d'expériences
Minitab permet d'analyser les données à partir des trois types d'expériences suivants :
| Type | La réponse dépend... |
| Mélange | des proportions relatives des composantes uniquement. |
| Variables de procédé de mélange | des composantes et des variables de procédé. Les variables de procédé sont des facteurs d'une expérience qui n'appartiennent pas au mélange mais qui peuvent affecter la réponse. |
| Quantités de mélange | des proportions relatives des composantes et de la quantité totale du mélange. |
Positionnement de points axiaux dans des plans accrus
Minitab accroît le plan (y ajoute des points) comme indiqué ci-dessous. Chaque point ajouté est à mi-chemin entre un sommet et le centre du plan.
Grâce à l'accroissement d'un plan, vous pouvez obtenir des informations sur les réponses à l'intérieur du plan, au lieu de prendre en compte uniquement les points placés sur les bordures.
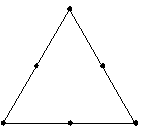
Sans accroissement
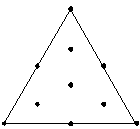
Avec accroissement
Conversion d'unités de composantes
Dans Minitab, vous pouvez créer des plans et analyser des données en unités de quantités, de proportions et de pseudo-composantes.
Pour convertir des données d'unités de proportions en unités de quantités, la formule est la suivante :
- Proportion = Quantité/Total
Si le total = 1, unités de proportions = unités de quantités.
Pour convertir des unités de proportions en unités de pseudo-composantes, la formule est la suivante :
- Pseudo = (proportion - borne inférieure)/(1 - somme des bornes inférieures)
- Proportion = pseudo * (1 - somme des bornes inférieures) + borne inférieure
Si toutes les bornes inférieures = 0, les unités de pseudo-composantes = unités de proportions
Termes du modèle
Les plans de mélange incluent plusieurs types de termes de modèle. Les termes et leurs représentations sont les suivantes :
| Modèle | Termes |
| Linéaire | A B C |
| Quadratique | Linéaire + AB AC BC |
| Cubique spécial | Quadratique + ABC |
| Cubique complet | Cubique spécial + AB(A-B) AC(A-C) BC(B-C) |
| Quartique spécial | Quadratique + AABC ABBC ABCC |
| Quartique complet | Quartique spécial + AB(A-B) AC(A-C) BC(B-C) AB(A-B)2 AC(A-C)2 BC(B-C)2 |
Les modèles de mélange ne contiennent aucun terme de constante. Les termes inverses incluent 1/A, 1/B, 1/C, etc.
