Sur ce thème
Coefficient (Coeff)
Minitab utilise l'estimation par les moindres carrés pour calculer les coefficients.
En termes matriciels, les estimations par les moindres carrés des coefficients sont les suivantes :
b = (X'X)-1X'y
Pour plus d'informations sur les coefficients des modèles d'ordre supérieur, reportez-vous à Cornell1.
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| y | colonne de réponse |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
Erreur type du coefficient (Coef ErT)
Pour la régression linéaire simple, l'erreur type du coefficient est la suivante :
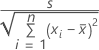
Les erreurs types des coefficients pour la régression multiple sont les racines carrées des éléments de diagonale de la matrice :
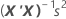
Notation
| Terme | Description |
|---|---|
| xi | ie valeur de prédicteur |
 | moyenne du prédicteur |
| X | matrice du plan |
| X' | transposition de la matrice du plan |
| s2 | carré moyen de l'erreur |
Valeur de t

Notation
| Terme | Description |
|---|---|
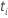 | statistique de test pour l' coefficient coefficient |
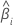 |  coefficient estimé coefficient estimé |
 | erreur type de l'  coefficient estimé coefficient estimé |
Valeur de p - Tableau des coefficients
La valeur de p bilatérale pour l'hypothèse nulle selon laquelle un coefficient de régression est égal à 0 est calculée comme suit :
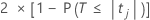
Les degrés de liberté pour l'erreur sont calculés comme suit :
n – p – 1
Notation
| Terme | Description |
|---|---|
 | fonction de répartition de la loi t, où le nombre de degrés de liberté est égal au nombre de degrés de liberté pour l'erreur |
| tj | statistique t du je coefficient |
| n | nombre d'observations dans l'ensemble de données |
| p | Somme des degrés de liberté pour les termes. |
Facteurs d'inflation de la variance (FIV)
Le FIV peut être obtenu en faisant régresser chaque prédicteur sur les prédicteurs restants et en notant la valeur R2.
Formule
Pour le prédicteur xj, le FIV est le suivant :

Notation
| Terme | Description |
|---|---|
| R2( xj) | coefficient de détermination avec xj comme variable de réponse et autres termes du modèle comme prédicteurs |
