Sur ce thème
Etape 1 : Déterminer si l'association entre la réponse et le terme est statistiquement significative
- Valeur de p ≤ α : l'association est statistiquement significative.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme.
- Valeur de p > α : l'association n'est pas statistiquement significative.
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme. Il est sans doute nécessaire de réajuster le modèle sans le terme.
Minitab n'affiche pas de valeurs de p pour les termes linéaires des composantes dans les expériences de mélanges en raison de la dépendance entre les composantes. Plus précisément, sachant que la somme des composantes doit atteindre une quantité donnée ou une proportion totale de 1, le fait de modifier l'une des composantes suffit à entraîner la modification des autres composantes. De plus, le modèle pour une expérience de mélanges n'inclut pas de constante, car elle est intégrée aux termes linéaires.
- Les termes d'interaction qui incluent uniquement des composantes indiquent que l'association entre le mélange de composantes et la réponse est statistiquement significative.
- Lorsque les coefficients des termes d'interaction sont positifs, cela implique que les composantes du terme agissent en synergie. En d'autres termes, la valeur de réponse moyenne est supérieure à celle que vous obtiendriez en calculant simplement la moyenne de la variable de réponse pour chaque mélange pur.
- Lorsque les coefficients des termes d'interaction sont négatifs, cela implique que les composantes du terme agissent de façon antagoniste. En d'autres termes, la valeur de réponse moyenne est inférieure à celle que vous obtiendriez en calculant simplement la moyenne de la variable de réponse pour chaque mélange pur.
- Les termes d'interaction qui incluent des composantes et les variables de procédé indiquent que l'effet des composantes sur la variable de réponse dépend des variables de procédé.
Conseil
Pour étudier plus en détail les relations des composantes et des variables de procédé avec la réponse, utilisez Graphique de contour, Diagramme de surface et Diagramme de tracé de réponse.
Coefficients de régression estimés pour Saveur (proportions de composante)
| Terme | Coeff | Coef ErT | Valeur de T | Valeur de p | FIV |
|---|---|---|---|---|---|
| Emmental | 104,874 | 0,667 | * | * | 15,94 |
| Gruyère | 175,08 | 5,89 | * | * | 203,46 |
| Bouillon | -8,810 | 0,659 | * | * | 26,04 |
| Emmental*Gruyère | 59,2 | 10,3 | 5,75 | 0,000 | 57,33 |
| Gruyère*Bouillon | 30,04 | 9,00 | 3,34 | 0,008 | 109,44 |
| Emmental*Température | 4,500 | 0,475 | 9,48 | 0,000 | 8,09 |
| Gruyère*Température | 4,500 | 0,679 | 6,62 | 0,000 | 2,71 |
| Bouillon*Température | 4,500 | 0,443 | 10,16 | 0,000 | 11,76 |
Résultats principaux : valeur de p, coefficients
Tous les termes d'interaction ont des valeurs de p inférieures au seuil de signification de 0,05.
Lorsque les coefficients des termes d'interaction ayant deux composantes sont positifs, cela signifie que les deux mélanges de composantes agissent en synergie. Le score moyen de saveur pour chaque mélange est supérieur à celui que vous obtiendriez en calculant simplement la moyenne des deux scores de saveur de chaque mélange pur.
De plus, l'interaction entre les ingrédients et la variable de procédé (la température) indique que le score de saveur du mélange dépend de la température de service.
Etape 2 : Déterminer l'ajustement du modèle à vos données
Pour déterminer l'ajustement du modèle aux données, étudiez les statistiques d'adéquation de l'ajustement dans le tableau Récapitulatif du modèle.
- S
-
Utilisez S pour évaluer la capacité du modèle à décrire la réponse. Utilisez S plutôt que les statistiques R2 pour comparer l'ajustement des modèles qui n'ont pas de constante.
S est mesuré en unités de la variable de réponse et représente la distance entre les valeurs de données et les valeurs ajustées. Plus S est petit, mieux le modèle décrit la réponse. Cependant, une faible valeur de S n'indique pas en soi que le modèle respecte les hypothèses du modèle. Vous devez examiner les graphiques des valeurs résiduelles pour vérifier les hypothèses.
- R carré
-
Plus la valeur R2 est élevée, plus le modèle est ajusté à vos données. R2 est toujours compris entre 0 et 100 %.
La valeur R2 augmente toujours lorsque vous ajoutez des prédicteurs à un modèle. Par exemple, le meilleur modèle à 5 prédicteurs aura toujours une valeur R2 au moins aussi élevée que celle du meilleur modèle à 4 prédicteurs. Par conséquent, R2 est surtout utile pour comparer des modèles de même taille.
- R carré (ajust)
-
Utilisez la valeur R2 ajusté pour comparer des modèles n'ayant pas le même nombre de prédicteurs. R2 augmente toujours lorsque vous ajoutez un prédicteur au modèle, même lorsque ce prédicteur n'apporte aucune amélioration réelle au modèle. La valeur de R2 ajusté intègre le nombre de prédicteurs dans le modèle pour vous aider à choisir le modèle correct.
- R carré (prév)
-
La valeur R2 prévu permet de déterminer la capacité de votre modèle à prévoir la réponse pour de nouvelles observations. Les modèles ayant des valeurs de R2 prévu élevées ont une meilleure capacité de prévision.
Une valeur de R2 prévu considérablement inférieure à R2 peut être un signe de surajustement du modèle. Un modèle est dit surajusté lorsqu'il inclut des termes pour des effets qui ne sont pas importants dans la population. Le modèle est alors spécialement ajusté aux données des échantillons, mais risque ne pas être utile pour effectuer des prévisions concernant la population entière.
La valeur R2 prévu peut également être plus utile que R2 ajusté pour comparer des modèles, car elle est calculée avec des observations qui ne sont pas incluses dans le calcul du modèle.
- Les petits échantillons ne fournissent pas d'estimation précise de la force de la relation entre la réponse et les prédicteurs. Pour obtenir une valeur R2 plus précise, vous devez utiliser un échantillon plus grand (en général, 40 ou plus).
- R2 n'est qu'une des mesures de l'ajustement du modèle aux données. Même si un modèle a une valeur R2 élevée, vous devez consulter les graphiques des valeurs résiduelles pour vérifier que le modèle respecte les hypothèses.
Récapitulatif du modèle
| S | R carré | R carré (ajust) | SomCar-ErrPrév | R carré (prév) |
|---|---|---|---|---|
| 0,276960 | 99,98% | 99,97% | 2,65322 | 99,93% |
Résultats principaux : S, R carré, R carré (ajust), R carré (prév)
Dans ces résultats, le modèle explique 99,98 % de la variation du degré de saveur. Pour ces données, la valeur de R2 indique que le modèle fournit un ajustement aux données correct. Si des modèles supplémentaires sont ajustés avec d'autres prédicteurs, utilisez les valeurs de R2 ajusté et les valeurs de R2 prévu pour comparer l'ajustement des modèles aux données.
Etape 3 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Graphiques des valeurs résiduelles pour la fonction Analyser un plan de mélange et cliquez sur le nom du graphique des valeurs résiduelles dans la liste située en haut de la page.
Graphique des valeurs résiduelles en fonction des valeurs ajustées
Les schémas du tableau suivant peuvent indiquer que le modèle n'est pas adapté.| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
Graphique des valeurs résiduelles en fonction de l'ordre
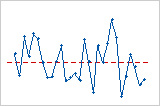
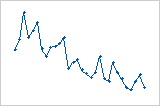
Tendance
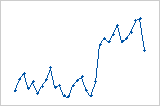
Equipe
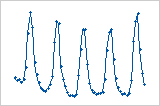
Cycle
Droite de Henry des valeurs résiduelles
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
Les schémas du tableau suivant peuvent indiquer que le modèle n'est pas adapté.
| Schéma | Ce que le schéma indique |
|---|---|
| Une ligne pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Modification de la pente | Une variable non identifiée |
