Sur ce thème
Valeur ajustée
Les valeurs ajustées sont notées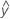 
. Les valeurs ajustées sont des estimations ponctuelles de la réponse moyenne pour des valeurs données des prédicteurs. Les valeurs des prédicteurs sont également appelées valeurs de x.
Interprétation
Les valeurs ajustées sont calculées en indiquant les valeurs de x correspondant à chaque observation de l'ensemble de données dans l'équation du modèle.
Par exemple, si l'équation est y = 5 + 10x, la valeur ajustée pour x = 2 est 25 (25 = 5 + 10(2)).
Les observations dont les valeurs ajustées sont très différentes de la valeur observée peuvent être des valeurs aberrantes. Les observations possédant des valeurs de prédicteurs aberrantes peuvent être influentes. Si Minitab détermine que vos données comprennent des valeurs aberrantes ou influentes, vos résultats comprennent le tableau Ajustements et diagnostics pour les observations aberrantes, qui indique quelles sont ces observations. Les observations aberrantes signalées par Minitab suivent mal l'équation de régression proposée. Toutefois, il est normal d'obtenir quelques observations aberrantes. Par exemple, selon les critères utilisés pour définir des valeurs résiduelles normalisées élevées, vous pouvez vous attendre à ce qu'environ 5 % de vos observations soient signalées pour leur valeur résiduelle normalisée importante. Pour plus d'informations sur les valeurs aberrantes, reportez-vous à la rubrique Observations aberrantes.
ErT ajust
L’erreur type de l’ajustement (ajustement SE) estime la variation de la réponse moyenne estimée pour les paramètres de variable spécifiés. Le calcul de l’intervalle de confiance pour la réponse moyenne utilise l’erreur type de l’ajustement. Les erreurs types sont toujours non négatives. L’analyse calcule les erreurs-types pour les Stat modèles du menu et les modèles de Regressão Linear et Regressão Logística Binária à partir du Module d'analyse prédictive.
Interprétation
Utilisez l'erreur type de l'ajustement pour mesurer la précision de l'estimation de la réponse moyenne. Plus l’erreur-type est petite, plus la réponse moyenne prédite est précise. Par exemple, un analyste développe un modèle pour prédire le délai de livraison. Pour un ensemble de paramètres variables, le modèle prédit un délai de livraison moyen de 3,80 jours. L’erreur type de l’ajustement pour ces paramètres est de 0,08 jour. Pour un deuxième ensemble de paramètres variables, le modèle produit le même délai de livraison moyen avec une erreur standard de l’ajustement de 0,02 jour. L’analyste peut être plus confiant dans le fait que le délai de livraison moyen pour le deuxième ensemble de paramètres variables est proche de 3,80 jours.
Avec la valeur ajustée, vous pouvez utiliser l’erreur type de l’ajustement pour créer un intervalle de confiance pour la réponse moyenne. Par exemple, en fonction du nombre de degrés de liberté, un intervalle de confiance à 95 % s’étend sur environ deux erreurs types au-dessus et en dessous de la moyenne prédite. Pour les délais de livraison, l’intervalle de confiance à 95 % pour la moyenne prédite de 3,80 jours lorsque l’erreur type est de 0,08 est (3,64, 3,96) jours. Vous pouvez être sûr à 95 % que la moyenne de la population se situe dans cette plage. Lorsque l’erreur-type est de 0,02, l’intervalle de confiance à 95 % est de (3,76, 3,84) jours. L’intervalle de confiance pour le deuxième ensemble de paramètres de variable est plus étroit car l’erreur standard est plus petite.
Val rés
Une valeur résiduelle (ei) est la différence entre une valeur observée (y) et la valeur ajustée correspondante (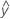
), qui est la valeur prévue par le modèle.
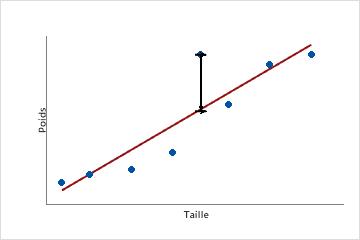
Ce nuage de points représente le poids d'un échantillon d'hommes adultes en fonction de leur taille. La droite de régression ajustée représente la relation entre la taille et le poids. Si la taille est égale à 6 pieds, la valeur ajustée pour le poids correspond à 190 livres. Si le poids réel est 200 livres, la valeur résiduelle est 10.
Interprétation
Représentez les valeurs résiduelles afin de déterminer si votre modèle est adapté et vérifie les hypothèses de régression. L'examen des valeurs résiduelles peut fournir des informations utiles sur l'ajustement du modèle aux données. En général, les valeurs résiduelles doivent être distribuées de manière aléatoire sans aucun schéma clair ni aucune valeur aberrante. Si Minitab détermine que vos données comprennent des observations aberrantes, il les indique dans les résultats, dans le tableau Ajustements et diagnostics pour les observations aberrantes. Les observations aberrantes signalées par Minitab suivent mal l'équation de régression proposée. Toutefois, il est normal d'obtenir quelques observations aberrantes. Par exemple, en vous fondant sur les critères de valeurs résiduelles élevées, vous pouvez vous attendre à ce qu'environ 5 % de vos observations soient signalées pour leur valeur résiduelle importante. Pour plus d'informations sur les valeurs aberrantes, reportez-vous à la rubrique Observations aberrantes.
Val. résid. norm
La valeur résiduelle normalisée est égale à la valeur résiduelle (ei) divisée par une estimation de son écart type.
Interprétation
Utilisez les valeurs résiduelles normalisées pour détecter les valeurs aberrantes. Les valeurs résiduelles normalisées supérieures à 2 et inférieures à −2 sont généralement considérées comme élevées. Le tableau Ajustements et diagnostics pour les observations aberrantes signale ces observations avec un "R". Les observations signalées par Minitab suivent mal l'équation de régression proposée. Toutefois, il est normal d'obtenir quelques observations aberrantes. Par exemple, selon les critères propres aux valeurs résiduelles normalisées élevées, vous pouvez vous attendre à ce qu'environ 5 % de vos observations soient signalées pour leur valeur résiduelle normalisée importante. Pour plus d'informations, reportez-vous à la rubrique Observations aberrantes.
Les valeurs résiduelles normalisées sont utiles car les valeurs résiduelles brutes peuvent ne pas indiquer de façon correcte les valeurs aberrantes. La variance de chaque valeur résiduelle brute peut varier selon la valeur de x qui lui est associée. Cette variation inégale complique l'évaluation de la grandeur des valeurs résiduelles brutes. La normalisation des valeurs résiduelles règle ce problème en convertissant les différentes variances sur une échelle commune.
