Méthodes et formules pour l'analyse de la variance pour la fonction Analyser la variabilité

Somme des carrés des distances. Les formules présentées sont destinées à un modèle factoriel complet à 2 facteurs comportant les facteurs A et B. Ces formules peuvent être étendues à des modèles comportant plus de 2 facteurs. Pour plus d'informations, reportez-vous à Montgomery¹.

La somme des carrés totale est la variation totale dans le modèle. SC (A) et SC (B) représentent la somme des écarts quadratiques des moyennes estimées des niveaux de facteurs par rapport à la moyenne globale. La somme des carrés de l'erreur (SC Erreur) est la somme des carrés des valeurs résiduelles. Cette valeur est également appelée erreur entre les traitements. Les calculs sont les suivants :

Si le modèle comporte des répliques, la somme des carrés de l'erreur pure est calculée comme suit :

Pour les cas autres que le modèle factoriel complet à 2 facteurs, vous pouvez utiliser une autre somme des carrés. Si vous ajustez un modèle réduit, de la somme des carrés pour l'inadéquation de l'ajustement est calculée comme suit :

Si le modèle comprend des points centraux, la somme des carrés pour la courbure est calculée comme suit :

Dans les plans en parcelles divisées, les sommes des carrés pour la variation de l'erreur de sous-bloc et de sous-parcelle sont calculés comme suit :

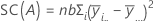
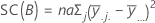
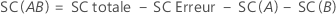
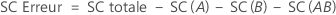
1. D.C. Montgomery (1991), Design and Analysis of Experiments, troisième édition, John Wiley & Sons.

Notation

Terme	Description
a	nombre de niveaux dans le facteur A
b	nombre de niveaux dans le facteur B
n	nombre total de répliques
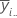	moyenne de l'ie niveau du facteur A
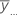	moyenne globale de toutes les observations
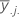	moyenne du je niveau du facteur B
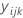	observation au ie niveau du facteur A, du je niveau du facteur B et de la ke réplique
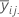	moyenne de l'ie niveau du facteur A et du je niveau du facteur B
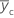	réponse moyenne pour les points centraux
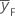	réponse moyenne pour les points factoriels
nF	nombre de points factoriels

Minitab répartit la composante de variance de la somme des carrés de la régression ou des traitements en sommes des carrés séquentielles pour chaque facteur. La somme des carrés séquentielle dépend de l'ordre dans lequel les facteurs ou les prédicteurs sont entrés dans le modèle. La somme des carrés séquentielle est la part de la somme des carrés de la régression expliquée par un facteur unique, en tenant compte de tous les autres facteurs déjà entrés.

Par exemple, dans le cas d'un modèle possédant trois facteurs ou prédicteurs X1, X2 et X3, la somme des carrés séquentielle pour X2 indique la proportion de la variation restante expliquée par X2, sachant que X1 figure déjà dans le modèle. Pour obtenir une séquence de facteurs différente, répétez l'analyse et entrez les facteurs dans un autre ordre.

Les sommes des carrés ajustées ne dépendent pas de l'ordre dans lequel les termes sont entrés dans le modèle. La somme des carrés ajustée est la proportion de variation expliquée par un terme, en tenant compte de tous les autres termes du modèle, indépendamment de l'ordre dans lequel ils ont été entrés.

Par exemple, dans le cas d'un modèle possédant trois facteurs X1, X2, et X3, la somme des carrés ajustée pour X2 indique la proportion de la variation restante expliquée par le terme de X2, du fait que les termes de X1 et X3 figurent également dans le modèle.

Les calculs des sommes des carrés ajustées pour trois facteurs sont les suivants :

• SCR (X3 | X1, X2) = SCE (X1, X2) - SCE (X1, X2, X3) ou
• SCR (X3 | X1, X2) = SCR (X1, X2, X3) - SCR (X1, X2)

où SCR (X3 | X1, X2) est la somme des carrés ajustée pour X3, sachant que X1 et X2 figurent dans le modèle.

• SCR (X2, X3 | X1) = SCE (X1) - SCE (X1, X2, X3) ou
• SCR (X2, X3 | X1) = SCR (X1, X2, X3) - SCR (X1)

où SCR (X2, X3 | X1) est la somme des carrés ajustée pour X2 et X3, sachant que X1 figure dans le modèle.

Vous pouvez étendre ces formules si votre modèle contient plus de 3 facteurs¹.

1. J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Pour un plan factoriel complet comportant les facteurs A et B, ainsi qu'une variable de blocage, le nombre de degrés de liberté associé à chaque somme des carrés est calculé comme suit :

Pour les interactions entre les facteurs, multipliez les degrés de liberté des facteurs du terme. Par exemple, si les facteurs sont A et B, les degrés de liberté de l'interaction AB sont calculés comme suit :

Pour calculer les degrés de liberté d'un type de terme, additionnez les degrés de liberté des termes. Par exemple, si les facteurs sont A et B, les effets principaux dans le modèle ont le nombre suivant de degrés de liberté :

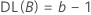
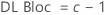
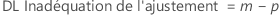
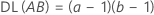
Pour les plans à deux niveaux avec des points centraux, le nombre de degrés de libertés pour la courbure est de 1.

Test permettant de déterminer si les effets principaux et les effets d'interaction sont significatifs. La formule des termes du modèle est la suivante :

Les degrés de liberté du test sont calculés comme suit :

• Numérateur = degrés de liberté du terme
• Dénominateur = degrés de liberté de l'erreur

Une valeur élevée de F est une indication en faveur du rejet de l'hypothèse nulle selon laquelle il n'existe aucun effet significatif.

Pour les plans en parcelles divisées équilibrés, la statistique F des facteurs difficiles à changer utilise le CM de l'erreur de sous-bloc comme dénominateur. Pour les autres plans en parcelles divisées, Minitab utilise une combinaison linéaire des erreurs SB et SP afin de créer un dénominateur reposant sur l'espérance mathématique des carrés moyens.