Un ingénieur qualité travaillant pour un fabricant de matériaux de construction développe un nouveau produit d'isolation. Il conçoit un plan factoriel complet à 2 niveaux pour étudier les effets de plusieurs facteurs sur la variabilité de la puissance de l'isolation. Tandis qu'il mène l'expérience relative à la puissance, l'ingénieur décide de collecter des échantillons supplémentaires pour étudier les effets des facteurs sur la variabilité dans la puissance d'isolation. L'ingénieur collecte six répétitions de mesure de puissance pour chaque combinaison de paramètres de facteur et calcule l'écart type des répétitions.
L'ingénieur analyse la variabilité d'un plan factoriel pour déterminer l'influence du type de matériau, de la pression d'injection, de la température d'injection et de la température de refroidissement sur la résistance de l'isolation.
- Ouvrez le fichier de données échantillons, PuissanceIsolation.MWX.
- Définissez l'option Exemple pour Prétraiter les réponses pour l'analyse de la variabilité.
- Sélectionnez .
- Dans la zone Réponse (écarts types), saisissez Std.
- Cliquez sur Termes.
- Dans Inclure les termes dans le modèle jusqu'à l'ordre, sélectionnez 2 dans la liste déroulante. Cliquez sur OK.
- Cliquez sur Graphiques.
- Sous Diagrammes des effets, sélectionnez Pareto.
- Sous Graphiques des valeurs résiduelles, sélectionnez Trois en un.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
Dans le tableau d'analyse de la variance, les valeurs de p pour l'effet principal Matériau et l'interaction Matériau*PressInj sont significatifs au niveau d'α de 0,05. L'ingénieur peut réduire le modèle.
La valeur R2 indique que le modèle explique 97,75 % de la variance de la puissance, ce qui indique qu'il est extrêmement bien ajusté aux données.
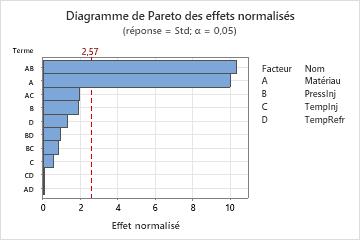
Le diagramme de Pareto vous permet de repérer visuellement les effets importants et de comparer l'importance relative des divers effets. De plus, vous pouvez voir que l'effet maximal est associé à l'interaction Matériau*PressInj (AB), car c'est celui qui a la barre la plus grande. L'interaction Matériau*TempRafr (AD) est la plus petite car c'est celle dont la barre est la plus courte.
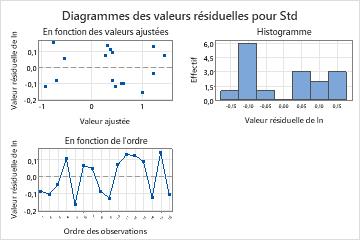
Ces graphiques ne signalent aucun problème concernant le modèle.
Méthode
| Estimation | Moindres carrés |
|---|
Coefficients codés pour ln(Std)
| Terme | Effet | Effet de rapport | Coeff | Coef ErT | Valeur de T | Valeur de p | FIV |
|---|---|---|---|---|---|---|---|
| Constante | 0,3424 | 0,0481 | 7,12 | 0,001 | |||
| Matériau | -0,9598 | 0,3830 | -0,4799 | 0,0481 | -9,99 | 0,000 | 1,00 |
| PressInj | -0,1845 | 0,8315 | -0,0922 | 0,0481 | -1,92 | 0,113 | 1,00 |
| TempInj | 0,0555 | 1,0571 | 0,0278 | 0,0481 | 0,58 | 0,589 | 1,00 |
| TempRefr | -0,1259 | 0,8817 | -0,0629 | 0,0481 | -1,31 | 0,247 | 1,00 |
| Matériau*PressInj | -0,9918 | 0,3709 | -0,4959 | 0,0481 | -10,32 | 0,000 | 1,00 |
| Matériau*TempInj | 0,1875 | 1,2062 | 0,0937 | 0,0481 | 1,95 | 0,109 | 1,00 |
| Matériau*TempRefr | 0,0056 | 1,0056 | 0,0028 | 0,0481 | 0,06 | 0,956 | 1,00 |
| PressInj*TempInj | -0,0792 | 0,9239 | -0,0396 | 0,0481 | -0,82 | 0,448 | 1,00 |
| PressInj*TempRefr | -0,0900 | 0,9139 | -0,0450 | 0,0481 | -0,94 | 0,392 | 1,00 |
| TempInj*TempRefr | 0,0066 | 1,0066 | 0,0033 | 0,0481 | 0,07 | 0,948 | 1,00 |
Récapitulatif du modèle pour ln(Std)
| S | R carré | R carré (ajust) | R carré (prév) |
|---|---|---|---|
| 0,549040 | 97,75% | 93,25% | 76,97% |
Analyse de la variance de ln(Std)
| Source | DL | SomCar ajust | CM ajust | Valeur F | Valeur de p |
|---|---|---|---|---|---|
| Modèle | 10 | 65,4970 | 6,5497 | 21,73 | 0,002 |
| Linéaires | 4 | 31,7838 | 7,9459 | 26,36 | 0,001 |
| Matériau | 1 | 30,0559 | 30,0559 | 99,71 | 0,000 |
| PressInj | 1 | 1,1104 | 1,1104 | 3,68 | 0,113 |
| TempInj | 1 | 0,1005 | 0,1005 | 0,33 | 0,589 |
| TempRefr | 1 | 0,5170 | 0,5170 | 1,71 | 0,247 |
| Interactions à 2 facteur(s) | 6 | 33,7132 | 5,6189 | 18,64 | 0,003 |
| Matériau*PressInj | 1 | 32,0953 | 32,0953 | 106,47 | 0,000 |
| Matériau*TempInj | 1 | 1,1466 | 1,1466 | 3,80 | 0,109 |
| Matériau*TempRefr | 1 | 0,0010 | 0,0010 | 0,00 | 0,956 |
| PressInj*TempInj | 1 | 0,2046 | 0,2046 | 0,68 | 0,448 |
| PressInj*TempRefr | 1 | 0,2642 | 0,2642 | 0,88 | 0,392 |
| TempInj*TempRefr | 1 | 0,0014 | 0,0014 | 0,00 | 0,948 |
| Erreur | 5 | 1,5072 | 0,3014 | ||
| Total | 15 | 67,0043 |
Equation de régression en unités non codées
| Ln(Std) | = | -1,30 - 0,158 Matériau + 0,0148 PressInj + 0,0180 TempInj + 0,0031 TempRefr - 0,01322 Matériau*PressInj + 0,01250 Matériau*TempInj + 0,00028 Matériau*TempRefr - 0,000141 PressInj*TempInj - 0,000120 PressInj*TempRefr + 0,000044 TempInj*TempRefr |
|---|
Structure des alias
| Facteur | Nom |
|---|---|
| A | Matériau |
| B | PressInj |
| C | TempInj |
| D | TempRefr |
| Alias |
|---|
| I |
| A |
| B |
| C |
| D |
| AB |
| AC |
| AD |
| BC |
| BD |
| CD |