Matrice du plan
Minitab utilise la même approche de la matrice du plan que pour le modèle linéaire général, qui utilise la régression pour ajuster le modèle spécifié. Minitab crée d'abord une matrice du plan d'expériences à partir des facteurs et du modèle que vous spécifiez. Les colonnes de cette matrice, appelée X, représentent les termes du modèle.
- Constante
- Covariables
- Blocs
- Facteurs
- Interactions
- Constante
- Covariable
- Facteur continu
Pour les blocs, le nombre de colonnes est égal au nombre de blocs moins un.
Facteurs de catégorie et interactions dans les plans à 2 niveaux
Dans un plan à 2 niveaux, le terme associé à un facteur de catégorie a une colonne. Chaque terme d'interaction a également une colonne.
Facteurs de catégorie dans les factoriels généraux
| Niveau de A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | -1 | -1 | -1 |
Interactions dans les plans factoriels généraux
Pour calculer le nombre de colonnes correspondant à un terme d'interaction, multipliez les colonnes correspondantes associées aux facteurs de l'interaction. Par exemple, supposons que A comporte 6 niveaux, C 3 niveaux et D 4 niveaux. Le terme A*C*D aura 5 x 2 x 3 = 30 colonnes. Pour obtenir les niveaux, multipliez chaque colonne associée à A par chaque colonne associée à C, puis par chaque colonne associée à D.
Colonnes de sous-blocs dans les plans en parcelles divisées
Remarque
Minitab n'analyse pas les plans en parcelles divisées avec une réponse binaire.
Pour un plan en parcelles divisées, Minitab utilise deux versions de la matrice de plan. L'une est la même que celle utilisée pour n'importe quel plan factoriel à 2 niveaux. L'autre inclut un bloc de colonnes qui représente les sous-blocs. Le calcul du terme d'erreur des sous-blocs, par exemple, utilise cette seconde version de la matrice de plan. Les colonnes correspondant aux sous-blocs suivent celles des facteurs difficiles à changer et des interactions impliquant des facteurs difficiles à changer.
Effets
Effets estimés de chaque facteur. Les effets sont uniquement calculés pour les modèles à 2 niveaux, mais pas pour les modèles factoriels généraux. La formule de l'effet d'un facteur est la suivante :
Effet = Coefficient * 2
Coefficients (Coeff)
Estimations des coefficients de régression de population dans une équation de régression. Pour chaque facteur, Minitab calcule k - 1 coefficients, où k correspond au nombre de niveaux dans le facteur. Pour un modèle factoriel complet à 2 niveaux et à 2 facteurs, les formules des coefficients pour les facteurs et les interactions sont les suivantes :


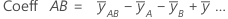
L'erreur type du coefficient pour ce modèle factoriel complet à 2 facteurs et à 2 niveaux est la suivante :

Pour plus d'informations sur les modèles comportant plus de deux facteurs ou des facteurs avec plus de deux niveaux, reportez-vous à Montgomery1.
Notation
| Terme | Description |
|---|---|
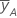 | moyenne de y au niveau supérieur du facteur A |
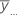 | moyenne globale de toutes les observations |
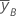 | moyenne de y au niveau supérieur du facteur B |
 | moyenne de y aux niveaux supérieurs des facteurs A et B |
| CME | carré moyen de l'erreur |
| n | nombre de - 1 et de 1 (dans la matrice de covariance) pour le terme estimé |
Transformation de Box-Cox
La transformation de Box-Cox sélectionne les valeurs lambda (comme indiqué ci-dessous) qui minimisent la somme des carrés des valeurs résiduelles. La transformation obtenue est Y λ lorsque λ ≠ 0, et ln(Y) lorsque λ = 0. Lorsque λ < 0, Minitab multiplie également la réponse transformée par −1 pour conserver l'ordre de la réponse non transformée.
Minitab recherche une valeur optimale entre −2 et 2. Les valeurs en dehors de cet intervalle sont susceptibles de ne pas fournir un meilleur ajustement.
Voici quelques transformations courantes dans lesquelles Y′ représente la transformation des données Y :
| Valeur lambda (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 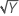 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Régression pondérée
La régression par les moindres carrés pondérée est une méthode permettant de traiter les observations qui présentent des variances non constantes. Si les variances ne sont pas constantes, attribuez :
- des pondérations relativement faibles aux observations ayant des variances importantes
- des pondérations relativement importantes aux observations ayant des variances faibles
Les pondérations sont généralement choisies comme l'inverse de la variance de l'erreur pure dans le réponse.
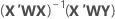
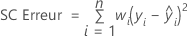
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| X' | transposition de la matrice de plan |
| W | matrice n x n, avec les pondérations sur la diagonale |
| Y | vecteur des valeurs de réponse |
| n | nombre d'observations |
| wi | pondération pour l'ie observation |
| yi | valeur de réponse pour l'ie observation |
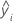 | valeur ajustée pour l'ie observation |
