Sur ce thème
DL
Le nombre total de degrés de liberté (DL) représente la quantité d'informations dans vos données. L'analyse utilise ces informations pour estimer les valeurs des paramètres de population inconnus. Le nombre total de DL est déterminé par le nombre d'observations dans votre échantillon. Les DL d'un terme affichent la quantité d'informations utilisée par ce terme. Le fait d'accroître l'effectif de l'échantillon permet d'obtenir davantage d'informations sur la population, ce qui augmente le nombre total de DL. Le fait d'augmenter le nombre de termes dans votre modèle utilise plus d'informations, ce qui réduit le nombre de DL disponibles pour l'estimation de la variabilité des estimations de paramètres.
- DL pour la courbure
- Si un plan comporte des points centraux, un DL est destiné au test de courbure. Si le terme des points centraux est compris dans le modèle, la ligne de la courbure fait partie du modèle. Si le terme des points centraux ne s'y trouve pas, la ligne de la courbure fait partie de l'erreur utilisée pour tester les termes présents dans le modèle.
- DL de l'erreur
- Si deux conditions sont remplies, Minitab subdivise les DL de l'erreur qui ne sont pas utilisés pour la courbure. La première condition est qu'il doit exister des termes que vous pouvez ajuster avec les données, mais qui ne sont pas inclus dans le modèle. Par exemple, si votre plan comporte des blocs, mais qu'ils ne sont pas dans le modèle. Le terme de point central est toujours réservé à la courbure, il ne compte donc pas comme un terme pouvant être ajusté avec les données, mais qui n'est pas dans le modèle en cours.
SomCar ajust
Les sommes des carrés ajustées sont des mesures de la variation des différentes composantes du modèle. L'ordre des prédicteurs dans le modèle n'a aucun effet sur le calcul des sommes des carrés ajustées. Dans le tableau Analyse de variance, Minitab divise les sommes des carrés en différentes composantes qui décrivent la variation due à différentes sources.
- SomCar ajust - Modèle
- La somme des carrés ajustée d'un modèle exprime la différence entre la somme totale des carrés et la somme des carrés d'erreur dans ce modèle, et permet de la comparer à celle d'un modèle qui utilise uniquement la moyenne de la réponse. Il s'agit de la somme de toutes les sommes des carrés séquentielles pour les termes du modèle.
- SomCar ajust - Groupes de termes
- La somme des carrés ajustée pour un groupe de termes du modèle correspond à la somme des carrés séquentielle pour tous les termes du groupe. Elle quantifie la part de variation des données de réponse expliquée par le groupe de termes.
- SomCar ajust - Terme
- La somme des carrés ajustée pour un terme représente l'augmentation de la somme des carrés du modèle obtenue par rapport à un modèle qui comporte uniquement les autres termes. Elle permet ainsi de quantifier la variation des données de réponse expliquée par chaque terme du modèle.
- SomCar ajust - Erreur
- La somme des carrés de l'erreur ajustée correspond à la somme des carrés des valeurs résiduelles. Elle quantifie la variation des données non expliquée par les prédicteurs.
- SomCar ajust - Courbure
- La somme des carrés ajustée pour la courbure peut être intégrée à la somme des carrés du modèle ou à la somme des carrés de l'erreur. Elle quantifie la part de la variation des données de réponse expliquée par le terme des points centraux. Cette variation représente l'effet combiné d'un ou de plusieurs termes quadratiques.
- SomCar ajust - Erreur pure
- La somme des carrés de l'erreur pure ajustée est intégrée à la somme des carrés d'erreur. La somme des carrés de l'erreur pure ajustée existe lorsqu'il existe des degrés de liberté d'erreur pure. Pour plus d'informations, reportez-vous à la section sur les degrés de liberté (DL). Elle quantifie la variation des données pour les observations avec les mêmes valeurs de facteurs, de blocs et de covariables.
- SomCar ajust - Total
- La somme totale des carrés ajustée correspond à la somme des carrés du modèle ajoutée à la somme des carrés d'erreur. Elle quantifie la variation totale dans les données.
Interprétation
Minitab utilise les sommes des carrés ajustées pour calculer les valeurs de p dans le tableau ANOVA. Minitab utilise aussi les sommes des carrés pour calculer la statistique R2. En général, vous interprétez les valeurs de p et la statistique R2 plutôt que les sommes des carrés.
CM ajust
Les carrés moyens ajustés mesurent la proportion de variation expliquée par un terme ou un modèle, en supposant que tous les autres termes sont dans le modèle, quel que soit l'ordre qu'ils y ont. Contrairement aux sommes des carrés ajustées, les carrés moyens ajustés tiennent compte des degrés de liberté.
Le carré moyen ajusté de l'erreur (également noté CME ou s2) est la variance autour des valeurs ajustées.
Interprétation
Minitab utilise les carrés moyens ajustés pour calculer les valeurs de p dans le tableau ANOVA. Minitab les utilise également pour calculer la statistique R2 ajusté. En général, vous interprétez les valeurs de p et la statistique R2 ajusté plutôt que les carrés moyens ajustés.
SomCar séq
Les sommes des carrés séquentielles sont des mesures de la variation des différentes composantes du modèle. Contrairement aux sommes des carrés ajustées, les sommes des carrés séquentielles dépendent de l'ordre des termes dans le modèle. Dans le tableau Analyse de variance, Minitab divise les sommes des carrés séquentielles en différentes composantes qui décrivent la variation due à différentes sources.
- SomCar séq - Modèle
- La somme des carrés séquentielle du modèle correspond à la différence entre la somme totale des carrés et la somme des carrés d'erreur. Il s'agit de la somme de toutes les sommes des carrés pour les termes du modèle.
- SomCar séq - Groupes de termes
- La somme des carrés séquentielle pour un groupe de termes du modèle correspond à la somme des sommes des carrés pour tous les termes du groupe. Elle quantifie la part de variation des données de réponse expliquée par le groupe de termes.
- SomCar séq - Terme
- La somme des carrés séquentielle pour un terme correspond à l'augmentation de la somme des carrés du modèle obtenue par rapport à un modèle qui compte uniquement les termes situés au-dessus dans le tableau ANOVA. Elle quantifie l'augmentation de la somme des carrés du modèle lorsque ce terme est ajouté à un modèle qui ne comporte pas les termes situés au-dessus.
- SomCar séq - Erreur
- La somme des carrés de l'erreur séquentielle correspond à la somme des carrés des valeurs résiduelles. Elle quantifie la variation des données non expliquée par les prédicteurs.
- SomCar séq - Courbure
- La somme des carrés séquentielle pour la courbure peut être intégrée à la somme des carrés du modèle ou à la somme des carrés de l'erreur. Elle quantifie la part de la variation des données de réponse expliquée par le terme des points centraux. Cette variation représente l'effet combiné d'un ou de plusieurs termes quadratiques.
- SomCar séq - Erreur pure
- La somme des carrés de l'erreur pure séquentielle est intégrée à la somme des carrés d'erreur. La somme des carrés de l'erreur pure ajustée existe lorsqu'il existe des degrés de liberté d'erreur pure. Pour plus d'informations, reportez-vous à la section sur les degrés de liberté (DL). Elle quantifie la variation des données pour les observations avec les mêmes valeurs de facteurs, de blocs et de covariables.
- SomCar séq - Total
- La somme totale des carrés séquentielle correspond à la somme des carrés du modèle ajoutée à la somme des carrés d'erreur. Elle quantifie la variation totale dans les données.
Interprétation
Minitab n'utilise pas les sommes des carrés séquentielles pour calculer les valeurs de p lorsque vous analysez un plan, mais peut utiliser les sommes des carrés séquentielles lorsque vous utilisez la fonction Ajuster le modèle de régression ou Ajuster le modèle linéaire général. En général, vous interprétez les valeurs de p et la statistique R2 en fonction de la somme des carrés ajustée.
Contribution
La contribution est le pourcentage de la somme des carrés séquentielle totale (SomCar séq) pouvant être attribué à chaque source figurant dans le tableau de l'analyse de la variance.
Interprétation
Plus les pourcentages sont élevés, plus la part de la variation de la réponse expliquée par la source est importante.
Valeur F
Une valeur F apparaît pour chaque test dans le tableau d'analyse de la variance.
- Valeur F pour le modèle
- La valeur F est une statistique de test utilisée pour déterminer si un terme du modèle est associé à la réponse, que ce soit des covariables, des blocs, des termes de facteurs ou la courbure.
- Valeur F pour des covariables en tant que groupe
- La valeur F est une statistique de test utilisée pour déterminer si certaines des covariables sont associées à la réponse simultanément.
- Valeur F pour des covariables individuelles
- La valeur F est une statistique de test utilisée pour déterminer si une covariable individuelle est associée à la réponse.
- Valeur F pour des blocs
- La valeur F est une statistique de test utilisée pour déterminer si la différence de conditions entre des blocs est associée à la réponse.
- Valeur F pour des types de termes de facteurs
- La valeur F est une statistique de test utilisée pour déterminer si un groupe de termes est associé à la réponse. Ces groupes de termes peuvent être, par exemple, des effets linéaires ou des interactions à 2 facteurs.
- Valeur F pour des termes individuels
- La valeur F est une statistique de test utilisée pour déterminer si le terme est associé à la réponse.
- Valeur F pour la courbure
- La valeur F est une statistique de test utilisée pour déterminer si la relation entre l'un des facteurs et la réponse est courbe.
- Valeur F pour le test d'inadéquation de l'ajustement
- La valeur F est une statistique de test utilisée pour déterminer s'il manque au modèle des termes comprenant les facteurs de l'expérience. Si vous enlevez des blocs ou des covariables du modèle en suivant une procédure pas à pas, le test d'inadéquation de l'ajustement inclut également ces termes.
Interprétation
Minitab utilise la valeur F pour calculer la valeur de p, qui vous permet de déterminer si le test est significatif d'un point de vue statistique. La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude. Une valeur F suffisamment élevée est synonyme de signification statistique.
Si vous souhaitez utiliser la valeur F pour savoir si l'hypothèse nulle doit être rejetée, comparez-la à votre valeur critique. Vous pouvez calculer la valeur critique dans Minitab ou rechercher la valeur critique dans un tableau de loi F, disponible dans la plupart des livres de statistiques. Pour plus d'informations sur la façon d'utiliser Minitab pour calculer la valeur critique, accédez à la rubrique Utilisation de la fonction de répartition (CDF) inverse et cliquez sur "Utiliser la CDF inverse pour calculer des valeurs critiques".
Valeur de p - Modèle
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Interprétation
Pour déterminer si le modèle explique la variation dans la réponse, comparez la valeur de p du modèle à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle pour le modèle est qu'il n'explique en rien la variation dans la réponse. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique 5 % de risques de conclure à tort que le modèle explique la variation dans la réponse.
- Valeur de p ≤ α : le modèle explique la variation dans la réponse
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que le modèle explique la variation dans la réponse.
- Valeur de p > α : vous n'êtes pas en mesure de conclure que le modèle explique la variation dans la réponse
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure que le modèle explique la variation dans la réponse. Il est sans doute nécessaire d'ajuster un nouveau modèle.
Valeur de p - Covariables
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Dans un plan d'expériences, les covariables représentent les variables mesurables mais difficilement contrôlables. Par exemple, les membres de l'équipe qualité d'un réseau hospitalier mettent en place une expérience en vue d'étudier la durée d'hospitalisation des patients admis pour une arthroplastie du genou. Pour l'expérience, l'équipe peut contrôler des facteurs tels que le format des consignes préopératoires. Pour éviter tout biais, l'équipe enregistre des données relatives aux covariables qu'elle ne peut pas contrôler, telles que l'âge des patients.
Interprétation
Pour déterminer si l'association entre la réponse et une covariable est statistiquement significative, comparez la valeur de p de la covariable à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle est que le coefficient de la covariable est égal à zéro, ce qui implique qu'il n'existe aucune association entre la covariable et la réponse.
En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort que des conditions différentes entre des essais modifient la réponse.
Lorsque vous évaluez la signification statistique de termes pour un modèle comportant des covariables, tenez compte des facteurs d'inflation de la variance (FIV).
- Valeur de p ≤ α : l'association est statistiquement significative
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la réponse et la covariable.
- Valeur de p > α : l'association n'est pas statistiquement significative
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la réponse et la covariable. Il est sans doute nécessaire d'ajuster un modèle sans la covariable.
Remarque
Toutes les valeurs FIV sont égales à 1 dans la plupart des plans factoriels, ce qui simplifie la détermination de la signification statistique. L'inclusion de covariables dans le modèle et l'occurrence d'essais ratés lors de la collecte de données sont deux situations courantes qui entraînent l'augmentation des FIV, ce qui complique l'interprétation de la signification statistique. Les valeurs des FIV se trouvent dans le tableau Coefficients. Pour plus d'informations, reportez-vous à la rubrique Tableau des coefficients pour la fonction Analyser un plan factoriel et cliquez sur FIV.
Valeur de p - Blocs
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Les blocs rendent compte des différences qui peuvent survenir entre des essais réalisés dans différentes conditions. Par exemple, un ingénieur crée une expérience dans le but d'étudier un procédé de soudage, mais il ne peut pas collecter toutes les données le même jour. La qualité de la soudure dépend de plusieurs variables qui changent chaque jour et que l'ingénieur ne peut pas contrôler, comme l'humidité relative. Pour prendre en compte ces variables non contrôlable, l'ingénieur regroupe les essais effectués chaque jour dans des blocs distincts. Ces blocs tiennent compte de la variation causée par des variables non contrôlables, afin que les effets de ces dernières ne soient pas confondus avec les effets des facteurs que l'ingénieur souhaite étudier. Pour plus d'informations sur la façon dont Minitab attribue des essais aux blocs, reportez-vous à la rubrique Qu'est-ce qu'un bloc ?.
Interprétation
Pour déterminer si des conditions différentes entre les essais modifient la réponse, comparez la valeur de p des blocs à votre seuil de signification afin d'évaluer l'hypothèse nulle. Cette dernière avance que la différence de conditions ne modifie pas la réponse.
En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort que des conditions différentes entre des essais modifient la réponse.
- Valeur de p ≤ α : la différence de conditions modifie la réponse
- Si la valeur de p est inférieure ou égale au seuil de signification, vous en concluez que la différence de conditions modifie la réponse.
- Valeur de p > α : vous n'êtes pas en mesure de conclure que la différence de conditions modifie la réponse
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas en conclure que la différence de conditions modifie la réponse. Il est sans doute nécessaire d'ajuster un modèle sans blocs.
Valeur de p - Facteurs, interactions et groupes de termes
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Interprétation
- Si une covariable est significative, vous pouvez en conclure que son coefficient est différent de zéro.
- Si un facteur de catégorie est significatif, vous pouvez en conclure que les moyennes des niveaux ne sont pas toutes égales.
- Si un terme d'interaction est significatif, vous pouvez en conclure que la relation entre un facteur et la réponse dépend des autres facteurs du terme.
Tests de groupes de termes
Si un groupe de termes est statistiquement significatif, vous pouvez en conclure qu'au moins un des termes dans le groupe a un effet sur la réponse. Lorsque vous vous fondez sur la signification statistique pour choisir les termes à conserver dans un modèle, vous n'enlevez généralement pas des groupes entiers de termes en même temps. La signification statistique de termes individuels peut varier selon les termes du modèle.
Analyse de la variance
| Source | DL | SomCar ajust | CM ajust | Valeur F | Valeur de p |
|---|---|---|---|---|---|
| Modèle | 10 | 447,766 | 44,777 | 17,61 | 0,003 |
| Linéaires | 4 | 428,937 | 107,234 | 42,18 | 0,000 |
| Matériau | 1 | 181,151 | 181,151 | 71,25 | 0,000 |
| PressInj | 1 | 112,648 | 112,648 | 44,31 | 0,001 |
| TempInj | 1 | 73,725 | 73,725 | 29,00 | 0,003 |
| TempRafr | 1 | 61,412 | 61,412 | 24,15 | 0,004 |
| Interactions à 2 facteur(s) | 6 | 18,828 | 3,138 | 1,23 | 0,418 |
| Matériau*PressInj | 1 | 0,342 | 0,342 | 0,13 | 0,729 |
| Matériau*TempInj | 1 | 0,778 | 0,778 | 0,31 | 0,604 |
| Matériau*TempRafr | 1 | 4,565 | 4,565 | 1,80 | 0,238 |
| PressInj*TempInj | 1 | 0,002 | 0,002 | 0,00 | 0,978 |
| PressInj*TempRafr | 1 | 0,039 | 0,039 | 0,02 | 0,906 |
| TempInj*TempRafr | 1 | 13,101 | 13,101 | 5,15 | 0,072 |
| Erreur | 5 | 12,712 | 2,542 | ||
| Total | 15 | 460,478 |
Dans ce modèle, le test des interactions à 2 facteurs n'est pas statistiquement significatif au seuil de 0,05. De même, aucun des tests pour les interactions à 2 facteurs n'est statistiquement significatif.
Analyse de la variance
| Source | DL | SomCar ajust | CM ajust | Valeur F | Valeur de p |
|---|---|---|---|---|---|
| Modèle | 5 | 442,04 | 88,408 | 47,95 | 0,000 |
| Linéaires | 4 | 428,94 | 107,234 | 58,16 | 0,000 |
| Matériau | 1 | 181,15 | 181,151 | 98,24 | 0,000 |
| PressInj | 1 | 112,65 | 112,648 | 61,09 | 0,000 |
| TempInj | 1 | 73,73 | 73,725 | 39,98 | 0,000 |
| TempRafr | 1 | 61,41 | 61,412 | 33,31 | 0,000 |
| Interactions à 2 facteur(s) | 1 | 13,10 | 13,101 | 7,11 | 0,024 |
| TempInj*TempRafr | 1 | 13,10 | 13,101 | 7,11 | 0,024 |
| Erreur | 10 | 18,44 | 1,844 | ||
| Total | 15 | 460,48 |
Si vous réduisez le modèle un terme après l'autre, en commençant par l'interaction à 2 facteurs qui a la valeur de p la plus élevée, la dernière interaction à 2 facteurs est statistiquement significative au seuil de 0,05.
Valeur de p - Courbure
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Minitab effectue un test pour déterminer la présence d'une courbure lorsque le plan comporte des points centraux. Le test étudie la moyenne ajustée de la réponse au niveau des points centraux par rapport à la moyenne attendue si les relations entre les termes du modèle et la réponse étaient linéaires. Pour visualiser la courbure, utilisez des diagrammes factoriels.
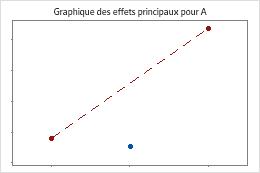
Les points centraux sont éloignés de la ligne qui joint les moyennes des sommets, ce qui suggère une relation courbe. Utilisez la valeur de p pour vérifier que cette courbure est statistiquement significative.
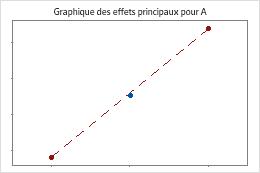
Les points centraux se trouvent près de la ligne qui joint les moyennes des sommets. La courbure n'est probablement pas statistiquement significative.
Interprétation
Pour déterminer si la relation entre au moins un des facteurs et la réponse est courbe, comparez la valeur de p de la courbure à votre seuil de signification afin d'évaluer l'hypothèse nulle. Cette dernière veut que toutes les relations entre les facteurs et la réponse sont linéaires.
En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort que des conditions différentes entre des essais modifient la réponse.
- Valeur de p ≤ α : la relation entre au moins un des facteurs et la réponse est courbe
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que la relation entre au moins un des facteurs et la réponse est courbe. Vous pouvez ajouter des points axiaux au plan afin de modéliser la courbure.
- Valeur de p > α : vous n'êtes pas en mesure de conclure que la relation entre un facteur et la réponse est courbe
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure que la relation entre l'un des facteurs et la réponse est courbe. Si la courbure est l'un des termes du modèle, vous pouvez réajuster le modèle sans terme pour les points centraux afin que la courbure soit intégrée à l'erreur.
Remarque
Si la courbure n'est pas statistiquement significative, vous pouvez généralement enlever le terme des points centraux. Si vous laissez les points centraux dans le modèle, Minitab suppose que le modèle contient une courbure que le plan factoriel ne peut pas ajuster. En raison de l'inadéquation de l'ajustement, le graphique de contour, le diagramme de surface et le graphique de contour superposé ne sont pas disponibles. En outre, Minitab n'effectue pas d'interpolation entre les niveaux de facteurs dans le plan avec la fonction Optimisation des réponses. Pour plus d'informations sur les différentes façons d'utiliser le modèle, reportez-vous à la rubrique Vue d’ensemble du modèle stocké.
Valeur de p - Inadéquation de l'ajustement
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Interprétation
- Valeur de p ≤ α : l'inadéquation de l'ajustement est statistiquement significative.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que le modèle ne rend pas correctement compte de la relation. Pour améliorer le modèle, vous devez peut-être ajouter des termes ou transformer vos données.
- Valeur de p > α : l'inadéquation de l'ajustement n'est pas statistiquement significative.
-
Si la valeur de p est supérieure au seuil de signification, le test ne détecte aucune inadéquation de l'ajustement.
