Analyse de la variance

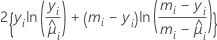
Le tableau de la somme des carrés d'écart est fondé sur le résultat général suivant, qui suppose que ϕ est connu. Si DI représente la somme des carrés d'écart associée à un modèle d'origine et DS représente la somme des carrés d'écart associée à un sous-ensemble de termes du modèle d'origine, sous certaines conditions de régularité, la relation suivante existe :

La différence entre les sommes des carrés d'écart est dispersée de manière asymptotique comme une loi du Khi deux avec d degrés de liberté. Ces statistiques sont calculées pour l'analyse (type III) ajustée et l'analyse (type I) séquentielle. La somme des carrés d'écart ajustée et la statistique du Khi deux dans le tableau des sommes des carrés d'écart sont égales. La somme des carrés d'écart de la moyenne ajustée correspond à la somme des carrés d'écart ajustée divisée par les degrés de liberté.
Pour l'analyse séquentielle, les résultats dépendent de l'ordre de saisie des prédicteurs dans le modèle. Le prédicteur n'explique que la somme des carrés d'écart séquentielle, s'il existe déjà des prédicteurs dans le modèle. Si vous disposez d'un modèle avec trois prédicteurs (X1, X2 et X3), la somme des carrés d'écart séquentielle pour X3 indique l'influence de X3 dans la somme des carrés d'écart restante, étant donné que X1 et X2 sont déjà présents dans le modèle. Pour obtenir une somme des carrés d'écart séquentielle différente, répétez la procédure de régression en saisissant les prédicteurs dans un autre ordre.
Si ϕ est inconnu, comme pour les réponses qui suivent une loi normale, la relation varie sous certaines conditions de régularité, comme suit :
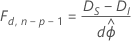
Dans le cas présent, la différence entre les sommes des carrés d'écart est dispersée de manière asymptotique sous forme de loi F avec d degrés de liberté pour le numérateur et n − p degrés de liberté pour le dénominateur. Pour estimer le paramètre de dispersion, utilisez le modèle d'origine.
Notation
| Terme | Description |
|---|---|
| yi | nombre d'événements pour la ie ligne |
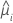 | réponse moyenne estimée de la ie ligne |
| mi | nombre d'essais pour la ie ligne |
| Lf | log de vraisemblance du modèle complet |
| Lc | log de vraisemblance du modèle avec un sous-ensemble de termes issus du modèle complet |
| d | les degrés de liberté représentent la différence entre le nombre de paramètres dans les modèles à comparer |
| ϕ | paramètre de dispersion, qui est de 1 pour le modèle binomial |
| n | nombre de lignes dans les données |
| p | degrés de liberté de la régression pour le modèle d'origine |
Degrés de liberté (DL)
| Source de variation | DL |
| Modèle | p |
| Erreur | n − p − 1 |
| Total | n − 1 |
| Prédicteurs continus | 1 |
| Prédicteurs de catégorie | q − 1 |
| Blocs | b − 1 |

Remarque
Pour les plans à deux niveaux avec des points centraux, le nombre de degrés de libertés pour la courbure est de 1.
Notation
| Terme | Description |
|---|---|
| p | Somme des degrés de liberté pour les prédicteurs. Les prédicteurs ne comprennent pas la constante. |
| n | Nombre de lignes dans le plan |
| q | Nombre de niveaux de prédicteur de catégorie |
| b | Nombre de blocs |
| a | Nombre de niveaux du facteur A |
| b | Nombre de niveaux du facteur B |
Log de vraisemblance
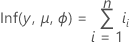
La forme générale des contributions individuelles est la suivante :

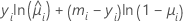
Notation
| Terme | Description |
|---|---|
| yi | nombre d'événements pour la ie ligne |
| mi | nombre d'essais pour la ie ligne |
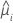 | réponse moyenne estimée de la ie ligne |
valeur de p (P)
Utilisée dans les tests d'hypothèse pour vous aider à décider de rejeter ou non une hypothèse nulle. La valeur de p est la probabilité d'obtenir une statistique de test au moins aussi extrême que la valeur réelle que vous avez calculée, si l'hypothèse nulle est vérifiée. Une valeur limite couramment utilisée pour la valeur de p est 0,05. Par exemple, si la valeur de p d'une statistique de test est inférieure à 0,05, rejetez l'hypothèse nulle.
