Méthode permettant de contrôler le niveau de confiance simultané de la totalité d'un ensemble d'intervalles de confiance. Il est important de prendre en considération le niveau de confiance simultané lors de l'examen de plusieurs intervalles de confiance, car la probabilité qu'au moins l'un des intervalles de confiance ne contienne pas le paramètre de population est plus grande pour un ensemble d'intervalles que pour n'importe quel intervalle unique. Pour contrecarrer ce taux d'erreur plus élevé, la méthode de Bonferroni ajuste le niveau de confiance de chacun des intervalles de manière à ce que le niveau de confiance simultané obtenu soit égal à la valeur que vous spécifiez.
Exemple pour les intervalles de confiance de Bonferroni
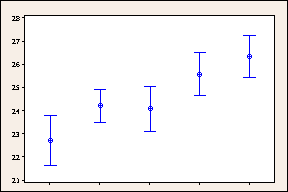
Intervalles de confiance à 95 % non ajustés pour les délais de livraison par centre d'expédition
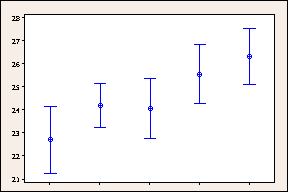
Intervalles de confiance de Bonferroni de 95 % pour les délais de livraison par centre d'expédition (intervalles de confiance individuels à 99 %)
Ces graphiques comparent les intervalles de confiance à 95 % classiques aux intervalles de confiance à 95 % de Bonferroni. Les intervalles de confiance plus larges de Bonferroni génèrent des estimations moins précises du paramètre de la population, mais limitent à un maximum de 5 % la probabilité qu'un ou plusieurs des intervalles de confiance ne contiennent pas le paramètre. A titre de comparaison, le taux d'erreur associé aux cinq intervalles de confiance à 95 % classiques est de 25 %.
Grâce à cette méthode prudente, le niveau de confiance global est d'au moins 1 - α. Pour obtenir un niveau de confiance global de 1 - α pour les estimations des intervalles de confiance bidimensionnelle, Minitab calcule chaque intervalle avec un niveau de confiance de (1 - α/g), où g représente le nombre d'intervalles. Dans les intervalles de Bonferroni, Minitab utilise des intervalles de confiance à 99 % (1,00 - 0,05/5 = 0,99) pour obtenir un niveau de confiance simultané de 95 %.
