Qu'est-ce que la MANOVA (Analyse multivariée de la variance) ?
- Puissance accrue
- Vous pouvez utiliser la structure de covariance des données entre les variables de réponse pour vérifier l'égalité des moyennes simultanément. Si les variables de réponse sont corrélées, ces informations supplémentaires permettent de détecter les différences qui sont trop petites pour être décelées par le biais d'une série d'ANOVA.
- Détection des modèles de réponse multivariés
- Les facteurs peuvent avoir une incidence sur la relation entre les réponses plutôt que sur une seule réponse. Les ANOVA ne détectent pas ces schémas multivariés, comme l'indiquent les figures suivantes.
- Contrôle du taux d'erreur
- La probabilité de rejeter à tort l'hypothèse nulle augmente à chaque ANOVA successive. L'exécution d'une seule MANOVA pour tester simultanément toutes les variables de réponse maintient le taux d'erreur égal au niveau d'alpha que vous avez défini.
Par exemple, supposons que vous analysiez l'impact de différents alliages (1, 2 et 3) sur la résistance et sur la souplesse des produits de bâtiment de votre entreprise. Dans un premier temps, vous effectuez deux ANOVA distinctes, mais les résultats ne sont pas significatifs, ce qui vous surprend. Vous tracez donc les données brutes des deux variables de réponse à l'aide de diagrammes de valeurs individuelles. Ces diagrammes confirment sous forme visuelle le caractère non significatif des résultats des ANOVA.
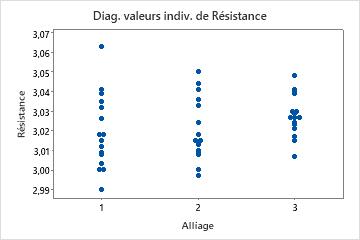
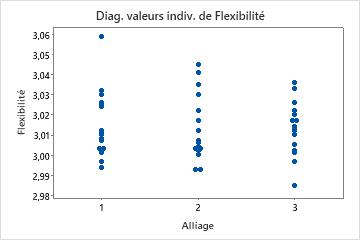
Etant donné que les variables de réponse sont corrélées, vous effectuez une MANOVA. Cette fois, les résultats sont significatifs avec des valeurs de p inférieures à 0,05. Vous créez un nuage de points afin de mieux comprendre les résultats.
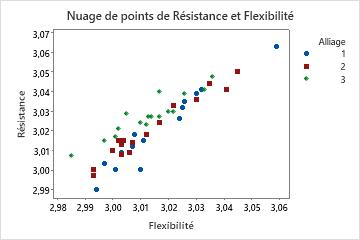
Les diagrammes de valeurs individuelles montrent, selon une perspective univariée, que les alliages n'affectent pas de manière significative la résistance ou la souplesse. Toutefois, le nuage de points des mêmes données montre que les différents alliages modifient la relation entre les deux variables de réponse. En d'autres termes, pour un score de souplesse donné, l'alliage 3 présente généralement un score de résistance plus élevé que les alliages 1 et 2. La MANOVA peut détecter ce type de réponse multivariée, contrairement à l'ANOVA.
Remarque
Généralement, il est recommandé de tracer les données avant d'effectuer une analyse, car cela permet de déterminer l'approche adaptée.
Quels tests multivariés sont compris dans l'analyse MANOVA ?
- Test de Wilk
- Test de Lawley-Hotelling
- Test de Pillai
- Test de la plus grande racine de Roy
- Une matrice H (pour Hypothèse) associée à chaque terme, également nommée sommes des carrés entre les échantillons
- Une matrice E (pour Erreurs) associée à l'erreur du test, également nommée sommes des carrés à l'intérieur des échantillons
Les matrices SSCP sont affichées lorsque vous demandez les matrices d'hypothèses.
Vous pouvez exprimer les statistiques de test en fonction de H, de E, de H et E, ou des valeurs propres de E-1 H. Vous pouvez choisir d'afficher ces valeurs propres. Si les valeurs propres sont répétées, les vecteurs propres correspondants ne sont pas uniques et, dans ce cas, les vecteurs propres affichés par Minitab et ceux apparaissant dans certains ouvrages ou autres logiciels peuvent ne pas concorder. En revanche, les tests de MANOVA sont toujours uniques.
