Qu'est-ce qu'une covariable ?
Les covariables sont généralement utilisées dans les ANOVA et les plans d'expériences. Dans ces modèles, une covariable peut désigner toute variable continue n'étant généralement pas contrôlée pendant la collecte de données. Le fait d'ajouter des covariables au modèle vous permet d'inclure et de prendre en compte des variables d'entrée qui ont été mesurées, mais qui n'ont été ni randomisées ni contrôlées dans le cadre de l'expérience. L'ajout de covariables peut améliorer considérablement l'exactitude du modèle et avoir une incidence significative sur les résultats de l'analyse finale. Inclure une covariable peut permettre de réduire l'erreur dans le modèle afin d'augmenter la puissance des tests de facteurs. Parmi les exemples de covariables courantes, on peut citer la température ambiante, l'humidité et les caractéristiques d'une pièce ou d'un sujet avant l'application d'un traitement.
Par exemple, un ingénieur veut étudier le niveau de corrosion sur quatre types de poutre en fer. Il expose chaque poutre à un traitement liquide afin d'accélérer la corrosion, mais il ne peut pas contrôler la température du liquide. La température est une covariable qui doit être prise en compte dans le modèle.
Dans le cadre d'un plan d'expériences, un ingénieur peut être intéressé par l'effet de la covariable de température ambiante sur le temps de séchage de deux types différents de peinture.
Exemple d'ajout de covariable à un modèle linéaire général
Une société de textiles utilise trois machines différentes pour fabriquer des fibres monofilament. Les ingénieurs qualité de la société souhaitent déterminer si la résistance à la rupture de la fibre diffère en fonction de la machine utilisée. Ils collectent des données relatives à la résistance et au diamètre de 5 fibres sélectionnées de façon aléatoire sur chaque machine. La résistance de la fibre étant liée à son diamètre, ils notent également le diamètre de la fibre pour l'utiliser éventuellement en tant que covariable.
| C1 | C2 | C3 |
|---|---|---|
| Machine | Diamètre | Résistance |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- Vérifiez que la relation entre la covariable et la réponse est linéaire. Pour ce faire, vous pouvez analyser les données à l'aide d'une droite d'ajustement dans Minitab.
- Sélectionnez .
- Dans la zone Réponse(Y), saisissez Résistance.
- Dans la zone Prédicteur(X), saisissez Diamètre.
- Examinez la distance à laquelle les données se trouvent par rapport à la droite d'ajustement et la proximité de R2 par rapport à un "ajustement parfait" (100 %).
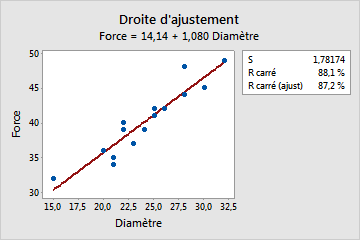
La droite d'ajustement indique une forte relation linéaire (87,2 %) entre le diamètre et la résistance.
- Effectuez l'analyse MLG avec la covariable.
- Sélectionnez .
- Dans la zone Réponses, saisissez Force.
- Dans la zone Facteurs, saisissez Machine.
- Dans la zone Covariables, saisissez Diamètre.
- Cliquez sur OK.
Pour les données relatives à la production de fibres, Minitab affiche les résultats suivants :
Modèle linéaire général : Force en fonction de Diamètre; Machine
Analyse de variance SomCar Valeur Source DL ajust CM ajust Valeur F de p Diamètre 1 178,014 178,014 69,97 0,000 Machine 2 13,284 6,642 2,61 0,118 Erreur 11 27,986 2,544 Inadéquation de l'ajustement 7 18,486 2,641 1,11 0,487 Erreur pure 4 9,500 2,375 Total 14 346,400La statistique F pour les machines est de 2,61 et la valeur de p de 0,118. La valeur de p étant supérieure à 0,05, vous ne pouvez pas rejeter l'hypothèse nulle selon laquelle la résistance des fibres ne diffère pas en fonction de la machine utilisée (avec un seuil de signification à 5 %). Vous pouvez supposer que la résistance des fibres est identique sur toutes les machines. Remarquez que la statique F pour le diamètre (covariable) est de 69,97 avec une valeur de p de 0,00. Ceci indique que l'effet de la covariable est significatif. Autrement dit, le diamètre a une influence statistiquement significative sur la résistance de la fibre.
A présent, supposons que vous effectuiez à nouveau l'analyse en omettant la covariable. Vous obtiendriez les résultats suivants :
Modèle linéaire général : Force en fonction de Machine
Analyse de variance SomCar Valeur Source DL ajust CM ajust Valeur F de p Machine 2 140,4 70,20 4,09 0,044 Erreur 12 206,0 17,17 Total 14 346,4Vous pouvez constater que la statistique F est de 4,09 avec une valeur de p de 0,044. Sans la covariable dans le modèle, vous rejetez l'hypothèse nulle à un seuil de signification de 5 % et concluez que la résistance des fibres diffère en fonction de la machine utilisée.
Cette conclusion est totalement contraire à celle obtenue lorsque vous avez effectué l'analyse avec la covariable. Cet exemple vous montre qu'il est possible d'obtenir des résultats d'analyses trompeurs si vous omettez d'inclure une covariable.
