Informations sur le message "déficience des rangs"
Les modèles linéaires sont dit à rang complet lorsqu'il existe un nombre adapté d'observations par combinaison de niveaux de facteurs pour pouvoir estimer tous les termes inclus dans le modèle. Lorsqu'il n'existe pas assez d'observations dans les données pour ajuster le modèle, Minitab supprime des termes jusqu'à ce que le modèle soit assez petit pour être ajusté aux données. Il est possible que d'autres modèles soient mieux ajustés aux données.
Supposons que vous ayez un modèle linéaire général à deux facteurs. Vous tentez d'ajuster le modèle avec les termes A B et A*B et un message d'erreur "déficience des rangs" apparaît. Ce message indique que le nombre d'observations par combinaison de niveaux de facteurs n'est pas suffisant. Essayez de supprimer le terme d'interaction (A*B).
Qu'est-ce que la déficience des rangs ?
La déficience des rangs est un problème qui peut empêcher Minitab d'effectuer des calculs de matrices. Prenons pour exemple l'ensemble de données suivant comportant deux variables de prévision et une variable de réponse :
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | Y |
| 1,5 | 9,7 | 15,0 |
| 1,4 | 8,4 | 14,0 |
| 1,6 | 8,6 | 16,0 |
| 1,7 | 8,9 | 17,0 |
| 1,7 | 8,1 | 14,5 |
X1 et X2 sont les variables de prédiction et Y la variable de réponse. L'analyse de régression de Minitab utilise les moindres carrés pour calculer les coefficients estimés b0, b1, b2, dans l'équation linéaire suivante :
Y = b0 + b1X1 + b2X2
La procédure des moindres carrés revient à résoudre l'ensemble des équations de matrice
b = (XTX)-1XTY
où b est un vecteur de colonne comportant les coefficients de modèles estimés, X est une matrice dont la première colonne est une colonne de valeurs égales à un (permettant d'estimer l'origine à l'ordonnée/la constante) et dont les colonnes restantes contiennent des données de prévision (X1, X2,…) et Y est le vecteur de colonne des données de réponses. Pour l'ensemble de données précédent, les matrices sont les suivantes :
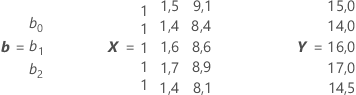
Minitab utilise la décomposition QR afin de calculer les estimations des paramètres (b0, b1 et b2), ainsi que leurs écarts types. Le calcul dépend des valeurs propres de la matrice (XTX). Si certaines valeurs propres de la matrice (XTX) sont essentiellement égales à zéro, la matrice carrée (XTX) est singulière, ou presque singulière, et Minitab ne pourra pas faire les calculs.
Quelle est l'origine de la déficience des rangs ?
La déficience des rangs survient si une colonne de variables X peut être écrite en tant que combinaison linéaire des autres colonnes X. Dans les deux exemples ci-dessous, les colonnes C1, C2 et C3 sont utilisées en tant que variables de prévision (X) :
Exemple 1
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 3 | 5 |
| 1,5 | 2,5 | 4 |
Exemple 2
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 4 | 5 |
| 1,5 | 3 | 4 |
Dans le premier exemple, vous pouvez remarquer que C1 + C2 = C3.
Dans le deuxième exemple, vous pouvez remarquer que 2*C1 = C2.
Si vous essayez d'effectuer une régression (ou une ANOVA) à l'aide de ces prédicteurs, Minitab supprimera des termes du modèle afin de pouvoir réaliser l'analyse.
La déficience des rangs peut également survenir avec des données de catégorie :
Exemple 3
| C1 | C2 | C3 |
|---|---|---|
| Machine | Opérateur | Réponse |
| 1 | Joel | 15 |
| 1 | Joel | 18 |
| 1 | Joel | 17 |
| 2 | Bill | 14 |
| 2 | Bill | 15 |
| 2 | Bill | 16 |
Dans cet exemple, vous pouvez remarquer que le schéma de la colonne "Machine" est exactement identique à celui de la colonne "Opérateur". Si vous effectuez une ANOVA avec cet ensemble de données, Minitab supprimera des termes du modèle afin d'effectuer l'analyse.
- Un terme d'interaction inclus ne possède pas au moins une observation pour chaque combinaison de niveaux de facteurs. Par exemple, si A possède 3 niveaux, B possède 4 niveaux et que vous incluez l'interaction A*B dans le modèle sans avoir au moins une observation pour chacune des 12 combinaisons de niveaux de facteurs.
- Il existe un emboîtement non équilibré.
- Une variable continue du modèle n'est pas définie en tant que covariable.
- Les degrés de liberté de l'erreur sont négatifs.
