Sur ce thème
Test de comparaisons multiples
Intervalles de comparaisons multiples pour un nombre d'échantillons k > 2
Soit 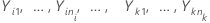 k échantillons indépendants, avec k >2, tous indépendants et distribués de façon identique avec une moyenne
k échantillons indépendants, avec k >2, tous indépendants et distribués de façon identique avec une moyenne 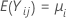 et une variance
et une variance  . Supposons en outre que les échantillons proviennent de populations présentant un aplatissement commun.
. Supposons en outre que les échantillons proviennent de populations présentant un aplatissement commun. 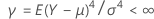
Et soit 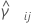 un estimateur d'aplatissement pour la paire d'échantillons (i, j) obtenu comme suit :
un estimateur d'aplatissement pour la paire d'échantillons (i, j) obtenu comme suit :
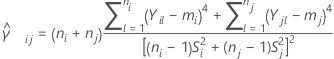
Soit 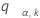 le point a le plus élevé de l'étendue de k variables indépendantes et distribuées de façon identique selon une loi de distribution normale standard et aléatoire. En d'autres termes,
le point a le plus élevé de l'étendue de k variables indépendantes et distribuées de façon identique selon une loi de distribution normale standard et aléatoire. En d'autres termes, 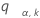 satisfait la condition suivante :
satisfait la condition suivante :
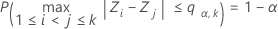
où Z1, ..., Zk sont des variables aléatoires indépendantes, distribuées de façon identique selon la loi normale standard. Barnard (1978) fournit un algorithme numérique simple fondé sur une quadrature de Gauss à 16 points pour calculer la fonction de répartition de l'étendue normale.
La procédure de comparaison multiple rejette l'analyse nulle d'égalité des variances (également appelée homogénéité des variances), si, et seulement si, les intervalles d'au moins une des paires suivantes ne se chevauchent pas :
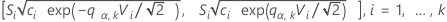
où
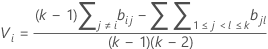
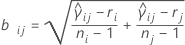
où ri = (ni - 3) / ni.
Nous désignons les intervalles ci-dessus par le terme intervalles de comparaisons multiples ou intervalles CM. Les intervalles CM de chaque échantillon ne doivent pas être interprétés comme des intervalles de confiance pour les écarts types des populations parentes. Hochberg et al. (1982) désignent ce genre d'intervalles servant à comparer des moyennes sous le terme "intervalles d'incertitude". Les intervalles de comparaisons multiples permettent seulement de comparer les écarts types ou les variances dans des plans à échantillons multiples. Lorsque le test général de comparaisons multiples est significatif, les écarts types correspondant aux intervalles qui ne se superposent pas sont statistiquement différents. (Pour en savoir plus sur la dérivation détaillée de ces intervalles, consultez le livre blanc sur les méthodes de comparaisons multiples.)
Intervalles de comparaisons multiples pour un nombre d'échantillons k = 2
Lorsqu'il n'existe que deux échantillons, les intervalles de comparaisons multiples sont obtenus avec la formule suivante :

où zα / 2 est le point du percentile supérieur α / 2 de la loi normale standard, ci = ni / ni - zα / 2 et Vi est donné par la formule suivante :
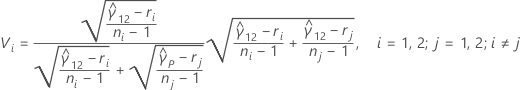
Valeur de p du test
Si le plan comporte 2 échantillons, Minitab calcule la valeur de p pour le test de comparaisons multiples à l'aide de la méthode de Bonett pour un test à 2 variances et un rapport hypothétisé, Ρo, de 1.
Si le plan comporte un nombre d'échantillons k > 2, soit Pi j la valeur de p du test pour toute paire (i, j) d'échantillons. La valeur de p pour la procédure de comparaisons multiples en tant que test général de l'égalité des variances est obtenue grâce à la formule suivante :

Pour plus d'informations, notamment des simulations et algorithmes détaillés pour le calcul de Pi j, consultez le livre blanc sur la méthode de Bonett, qui contient des simulations et d'autres renseignements.
Notation
| Terme | Description |
|---|---|
| ni | nombre d'observations dans l'échantillon i |
| Y i l | le observation de l'échantillon i |
| mi | moyenne tronquée pour l'échantillon i avec des proportions de troncage de  |
| k | nombre d'échantillons |
| Si | écart type de l'échantillon i |
| α | seuil de signification pour le test = 1 - (niveau de confiance / 100) |
| Ci | 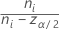 |
| Zα / 2 | point de percentile supérieur α/2 de la loi normale standard |
| ri |  |
Statistique du test de Levene
Minitab affiche une statistique de test et une valeur de p pour le test de Levene. L'hypothèse nulle est que les variances sont égales et l'hypothèse alternative est que les variances ne sont pas égales. Utilisez le test de Levene lorsque les données sont issues de lois de distribution continues, mais pas nécessairement normales.
La méthode de calcul pour le test de Levene est une modification de la procédure de Levene (Levene, 1960) qui a été mise au point par Brown et Forsythe (1974). Cette méthode prend en compte les distances des observations par rapport à la médiane de l'échantillon, et non à la moyenne. Le fait d'utiliser la médiane au lieu de la moyenne de l'échantillon rend le test plus robuste pour des échantillons plus petits et rend la procédure asymptotiquement indépendante de toute loi. Si la valeur de p est inférieure au seuil α, vous devez rejeter l'hypothèse nulle d'égalité des variances.
Formule
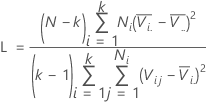
- H. Levene (1960). Contributions to Probability and Statistics. Stanford University Press, CA.
- M. B. Brown et A. B. Forsythe (1974). "Robust tests for the equality of variance," Journal of the American Statistical Association, 69, 364-367.
Notation
| Terme | Description |
|---|---|
| Vij |  |
| i | 1, ..., k |
| j | 1, ..., ni |
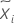 | médiane |
Statistique du test de Bartlett
Minitab affiche une statistique de test et une valeur de p pour le test de Bartlett. Lorsqu'il n'existe que deux niveaux, Minitab effectue un test F plutôt qu'un test de Bartlett. Pour ces tests, l'hypothèse nulle est que les variances sont égales et l'hypothèse alternative est que les variances ne sont pas égales. Utilisez le test de Bartlett lorsque les données sont issues de lois normales ; ce test n'est pas robuste en cas d'écart par rapport à la normalité.
La statistique du test de Bartlett calcule la moyenne arithmétique pondérée et la moyenne géométrique pondérée de la variance de chaque échantillon en fonction des degrés de liberté. Plus la différence dans les moyennes est importante, moins il est probable que les variances d'échantillons soient égales. B suit une loi de loi du χ2 à k – 1 degrés de liberté. Si la valeur de p est inférieure au seuil α, vous devez rejeter l'hypothèse nulle d'égalité des variances.
Formule
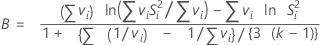
Notation
| Terme | Description |
|---|---|
| si2 |  |
| k | nombre d'échantillons |
| vi | ni - 1 |
| ni | nombre d'observations à l'ie niveau de facteur |
Statistique de test F
Lorsqu'il n'existe que deux niveaux, Minitab effectue un test F plutôt qu'un test de Bartlett. L'hypothèse nulle est que les variances sont égales et l'hypothèse alternative est que les variances ne sont pas égales. Utilisez la statistique F lorsque les données obéissent à une loi normale.
Si la valeur de p est inférieure au seuil α, vous devez rejeter l'hypothèse nulle d'égalité des variances.
Formule
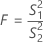
Formule pour la valeur de p
- Pour un test unilatéral avec une hypothèse alternative de type "inférieur à", la valeur de p est égale à la probabilité d'obtenir une statistique F inférieure ou égale à la valeur observée d'après une distribution F avec des degrés de liberté DL1 et DL2.
- Pour un test bilatéral, où le rapport est inférieur à 1, la valeur de p est égale à deux fois la zone située sous la courbe F, inférieure à la valeur observée selon une distribution F avec des degrés de liberté DL1 et DL2.
- Pour un test bilatéral, où le rapport est supérieur à 1, la valeur de p est égale à deux fois la zone située sous la courbe F, supérieure à la valeur observée selon une distribution F avec des degrés de liberté DL1 et DL2.
- Pour un test unilatéral avec une hypothèse alternative de type "supérieur à", la valeur de p est égale à la probabilité d'obtenir une statistique F supérieure ou égale à la valeur observée d'après une distribution F avec des degrés de liberté DL1 et DL2.
Notation
| Terme | Description |
|---|---|
| S12 | variance de l'échantillon 1 |
| S22 | variance de l'échantillon 2 |
| n1 - 1 | degrés de liberté pour le numérateur |
| n2 - 1 | degrés de liberté pour le dénominateur |
Ecart type (EcTyp)
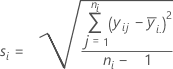
Notation
| Terme | Description |
|---|---|
| yij | observations à l'ie niveau de facteur |
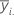 | moyenne des observations à l'ie niveau de facteur |
| ni | nombre d'observations à l'ie niveau de facteur |
Intervalles de confiance de Bonferroni
Minitab calcule les intervalles de confiance pour les écarts types avec la méthode de Bonferroni. Un intervalle de confiance est une étendue de valeurs ayant de fortes chances de contenir un paramètre de population, dans ce cas, l'écart type.
Les intervalles de confiance d'écart type sont calculés en utilisant un niveau de confiance de 1 – α / 2. La méthode de Bonferroni utilise le niveau de confiance 1 – α / 2p pour chaque intervalle de confiance individuel, où p représente le nombre de combinaisons de facteur et de niveau. Cette méthode garantit que l'ensemble d'intervalles de confiance a un niveau de confiance d'au moins 1 – α. La méthode de Bonferroni produit des intervalles de confiance plus prudents (plus larges), ce qui réduit la probabilité d'erreur de 1ère espèce.
