Sur ce thème
Etape 1 : Estimer l'écart type de chaque population
Utilisez les intervalles de confiance de Bonferroni pour estimer l'écart type de chaque population en fonction de vos facteurs de catégorie. L'intervalle de confiance est une étendue de valeurs probables de l'écart type de la population correspondante.
Minitab ajuste les intervalles de confiance de Bonferroni de manière à maintenir le niveau de confiance simultané. Avec les intervalles de confiance de Bonferroni à 95 %, vous pouvez être sûr à 95 % que la totalité de l'ensemble d'intervalles de confiance inclut les écarts types de population réels pour tous les groupes.
Le contrôle du niveau de confiance simultané est particulièrement important lorsque vous réalisez des comparaisons multiples. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas l'écart type réel augmente avec le nombre d'intervalles de confiance.
Remarque
Vous ne pouvez pas utiliser les intervalles de confiance de Bonferroni pour déterminer si les différences entre les paires de groupes sont statistiquement significatives. Pour déterminer la signification statistique des différences entre les paires de groupes, utilisez les intervalles de comparaison multiple de l'étape 2.
Pour plus d'informations, reportez-vous aux rubriques Utilisation des niveaux de confiance pour déterminer les différences significatives entre des niveaux de facteurs dans des comparaisons multiples et Qu'est-ce que la méthode de Bonferroni ?
Méthode
| Hypothèse nulle | Toutes les variances sont égales |
|---|---|
| Hypothèse alternative | Au moins une variance est différente |
| Seuil de signification | α = 0,05 |
Intervalles de confiance de Bonferroni à 95 % pour les écarts types
| Engrais | N | EcTyp | IC |
|---|---|---|---|
| RapidPouss | 50 | 4,28743 | (3,43659; 5,61790) |
| Aucun | 50 | 5,09137 | (4,24793; 6,40914) |
| Superplante | 49 | 5,49969 | (4,48577; 7,08914) |
Résultats principaux : EcTyp, intervalles de confiance de Bonferroni à 95 %, niveau de confiance individuel
Dans ces résultats, les intervalles de confiance de Bonferroni indiquent que vous pouvez être sûr à 95 % que la totalité de l'ensemble d'intervalles de confiance inclut les écarts types de population réels pour tous les groupes. De plus, le niveau de confiance individuel indique le degré de certitude avec lequel vous pouvez supposer qu'un intervalle de confiance individuel contient l'écart type de la population du groupe spécifique. Par exemple, vous pouvez être sûr à 98,3333 % que l'écart type de la population RapidPouss se trouve dans l'intervalle de confiance (3,43659 ; 5,6179).
Etape 2 : Déterminer si les écarts types de population diffèrent
Utilisez le graphique récapitulatif pour déterminer si certaines différences entre les écarts types sont statistiquement significatives. Les types de tests et d'intervalles affichés par Minitab dépendent de si vous avez coché Utiliser le test en considérant une loi normale dans la sous-boîte de dialogue Options, ainsi que du nombre de groupes dans vos données.
- Valeurs de p pour les tests
-
Utilisez les valeurs de p du graphique récapitulatif pour déterminer si certaines différences entre les écarts types sont statistiquement significatives. Minitab affiche les résultats d'un ou deux tests évaluant l'égalité des variances. Si vous disposez de deux valeurs de p non concordantes, reportez-vous à la rubrique Toutes les statistiques et tous les graphiques et cliquez sur "Tests" pour savoir lequel utiliser.
Comparez la valeur de p au seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle stipule que les écarts types des groupes sont tous égaux. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'une différence existe.
Suivez les règles ci-après pour interpréter les valeurs de p :- Si la valeur de p est supérieure à α, les différences entre les écarts types ne sont pas statistiquement significatives.
- Si la valeur de p est inférieure ou égale à α, les différences entre certains écarts types sont statistiquement significatives.
- Les intervalles de comparaisons multiples
-
Si vous n'avez pas sélectionné Utiliser le test en considérant une loi normale, le graphique récapitulatif affiche les intervalles de confiance pour la méthode de comparaisons multiples. En général, vous pouvez fonder vos conclusions sur le test et les intervalles de comparaisons multiples, sauf si vous disposez de petits échantillons provenant de lois très asymétriques ou à queues lourdes.
Utilisez les intervalles de comparaisons multiples pour repérer des paires spécifiques d'écarts types qui sont inégaux. Si deux intervalles ne se chevauchent pas, la différence entre les écarts types correspondants est statistiquement significative. Si la valeur de p pour le test de comparaisons multiples est inférieure au seuil de signification, les intervalles d'au moins une paire ne se chevauchent pas.
- Intervalles de confiance de Bonferroni
-
Si vous avez sélectionné Utiliser le test en considérant une loi normale, le graphique récapitulatif affiche les intervalles de confiance de Bonferroni pour estimer l'écart type de chaque population. Vous ne pouvez pas utiliser ces intervalles pour déterminer si les différences entre les paires de groupes sont statistiquement significatives. Reportez-vous à l'étape 1 pour savoir comment interpréter les intervalles de confiance de Bonferroni.
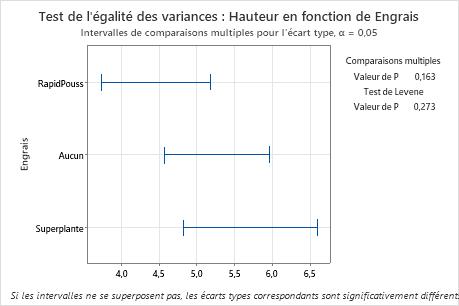
Résultats principaux : valeur de p du test de comparaisons multiples
Dans ce graphique récapitulatif, la valeur de p pour le test des comparaisons multiples est supérieure au seuil de signification de 0,05. Aucune des différences entre les groupes n'est statistiquement significative et tous les intervalles de comparaisons se chevauchent.
