Sur ce thème
Hypothèse nulle, hypothèse alternative
Le test de l'égalité des variances est un test d'hypothèse qui évalue deux affirmations relatives à plusieurs écarts types de population qui s'excluent mutuellement. Ces deux affirmations sont appelées "hypothèse nulle" et "hypothèse alternative". Un test d'hypothèse utilise des données échantillons pour déterminer si l'hypothèse nulle peut être rejetée.
- Hypothèse nulle (H0)
- L'hypothèse nulle stipule que les écarts types de population sont tous égaux.
- Hypothèse alternative (HA)
- L'hypothèse alternative stipule que tous les écarts types de population ne sont pas égaux.
Interprétation
Pour savoir si l'hypothèse nulle doit être rejetée, comparez la valeur de p au seuil de signification.
N
L'effectif de l'échantillon (N) est le nombre total d'observations dans chaque groupe.
Interprétation
L'effectif de l'échantillon a une influence sur l'intervalle de confiance et la puissance du test.
En général, plus l'échantillon est grand, plus l'intervalle de confiance est étroit. En outre, un effectif d'échantillon plus grand donne au test plus de puissance pour détecter une différence.
Ecart type (EcTyp)
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données autour la moyenne. Le symbole σ (sigma) représente souvent l'écart type d'une population. La lettre s est souvent utilisée pour représenter l'écart type d'un échantillon.
Interprétation
L'écart type utilise les mêmes unités que la variable. Une valeur d'écart type élevée indique que les données sont dispersées. D'une manière générale, pour une loi normale, environ 68 % des valeurs se situent à moins d'un écart type de la moyenne, 95 % des valeurs se situent à moins de deux écarts types et 99,7 % des valeurs se situent à moins de trois écarts types.
Intervalles de confiance de Bonferroni
Utilisez les intervalles de confiance de Bonferroni pour estimer l'écart type de chaque population en fonction de vos facteurs de catégorie. Chaque intervalle de confiance est une étendue de valeurs ayant de fortes chances de contenir l'écart type de la population correspondante. Minitab ajuste les intervalles de confiance de Bonferroni de manière à maintenir le niveau de confiance simultané.
Le contrôle du niveau de confiance simultané est particulièrement important lorsque vous évaluez plusieurs intervalles de confiance. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas l'écart type réel augmente avec le nombre d'intervalles de confiance.
Pour plus d'informations, reportez-vous aux rubriques Présentation des niveaux de confiance individuel et simultané dans les comparaisons multiples et Qu'est-ce que la méthode de Bonferroni ?
Remarque
Vous ne pouvez pas utiliser ces intervalles de confiance de Bonferroni pour déterminer si les différences entre des paires de groupes sont statistiquement significatives. Pour cela, vous devez utiliser les valeurs de p et les intervalles de confiance des comparaisons multiples du graphique récapitulatif.
Interprétation
Méthode
| Hypothèse nulle | Toutes les variances sont égales |
|---|---|
| Hypothèse alternative | Au moins une variance est différente |
| Seuil de signification | α = 0,05 |
Intervalles de confiance de Bonferroni à 95 % pour les écarts types
| Engrais | N | EcTyp | IC |
|---|---|---|---|
| RapidPouss | 50 | 4,28743 | (3,43659; 5,61790) |
| Aucun | 50 | 5,09137 | (4,24793; 6,40914) |
| Superplante | 49 | 5,49969 | (4,48577; 7,08914) |
Dans ces résultats, les intervalles de confiance de Bonferroni à 95 % indiquent que vous pouvez être sûr à 95 % que la totalité de l'ensemble d'intervalles de confiance inclut les écarts types de population réels pour tous les groupes. De plus, le niveau de confiance individuel indique le degré de certitude avec lequel vous pouvez supposer qu'un intervalle de confiance individuel contient l'écart type de la population du groupe spécifique. Par exemple, vous pouvez être sûr à 98,3333 % que l'écart type de la population RapidPouss se trouve dans l'intervalle de confiance (3,43659 ; 5,6179).
Niveau de confiance individuel
Le niveau de confiance individuel est le pourcentage de fois qu'un même intervalle de confiance contient l'écart type réel pour un groupe spécifique, si l'étude est répétée plusieurs fois.
La probabilité qu'au moins un intervalle de confiance ne contienne pas l'écart type réel augmente avec le nombre d'intervalles de confiance dans un ensemble. Le niveau de confiance simultané indique le degré de certitude avec lequel vous pouvez supposer que la totalité de l'ensemble d'intervalles de confiance contient les écarts types réels de la population pour tous les groupes.
Interprétation
Méthode
| Hypothèse nulle | Toutes les variances sont égales |
|---|---|
| Hypothèse alternative | Au moins une variance est différente |
| Seuil de signification | α = 0,05 |
Intervalles de confiance de Bonferroni à 95 % pour les écarts types
| Engrais | N | EcTyp | IC |
|---|---|---|---|
| RapidPouss | 50 | 4,28743 | (3,43659; 5,61790) |
| Aucun | 50 | 5,09137 | (4,24793; 6,40914) |
| Superplante | 49 | 5,49969 | (4,48577; 7,08914) |
Vous pouvez être sûr à 98,3333 % que chaque intervalle de confiance individuel contient l'écart type de la population pour le groupe spécifique. Par exemple, vous pouvez être sûr à 98,3333 % que l'écart type de la population RapidPouss se trouve dans l'intervalle de confiance (3,43659 ; 5,6179). Toutefois, comme l'ensemble comprend trois intervalles de confiance, vous ne pouvez être sûr qu'à 95 % que tous les intervalles contiennent les valeurs réelles.
Tests
Les types de tests d'égalité des variances affichés par Minitab dépendent de si vous avez sélectionné Utiliser le test en considérant une loi normale dans la sous-boîte de dialogue Options, ainsi que du nombre de groupes dans vos données.
Méthodes de Levene et de comparaisons multiples
Si vous n'avez pas sélectionné Utiliser le test en considérant une loi normale, Minitab affiche les résultats de test pour la méthode de comparaisons multiples et pour celle de Levene. Pour la plupart des lois continues, ces deux méthodes indiquent un taux d'erreur de 1ère espèce proche du seuil de signification spécifié (noté alpha ou α). La méthode de comparaisons multiples est généralement plus puissante. Si la valeur de p pour la méthode de comparaisons multiples est significative, vous pouvez utiliser le diagramme récapitulatif pour identifier des populations spécifiques dont les écarts types diffèrent les uns des autres.
- Vos échantillons contiennent chacun moins de 20 observations.
- La loi de distribution d'une ou de plusieurs des populations est très asymétrique, ou ses queues sont lourdes. Contrairement à la loi normale, une loi à queues lourdes comporte un plus grand nombre de données à ses extrémités inférieure et supérieure.
Si la valeur de p pour le test de comparaisons multiples est inférieure au seuil de signification choisi, les différences entre certains écarts types sont statistiquement significatives. Utilisez les intervalles de comparaisons multiples pour déterminer les écarts types qui sont significativement différents les uns par rapport aux autres. Si deux intervalles ne se chevauchent pas, les écarts types (et les variances) correspondants sont significativement différents.
Lorsque vous disposez de petits échantillons provenant de lois très asymétriques ou à extrémités lourdes, le taux d'erreur de 1ère espèce pour la méthode de comparaisons multiples peut être supérieur à α. Dans ces conditions, si la méthode de Levene vous donne une valeur de p plus faible que la méthode de comparaisons multiples, vous devez fonder vos conclusions sur la méthode de Levene.
Test F, test de Bartlett
Si vous sélectionnez Utiliser le test en considérant une loi normale et que vous disposez de deux groupes, Minitab effectue un test F. Si vous disposez d'au moins 3 groupes, Minitab effectue un test de Bartlett.
Le test F et le test de Bartlett ne sont exacts qu'avec des données normalement distribuées. En cas d'écart par rapport à la normalité, ces tests peuvent générer des résultats inexacts. Toutefois, si les données suivent la loi normale, le test F et le test de Bartlett sont généralement plus puissants que la méthode de comparaisons multiples ou la méthode de Levene.
Si la valeur de p du test est inférieure au seuil de signification, les différences entre certains écarts types sont statistiquement significatives.
Statistique du test
Remarque
Le test de comparaisons multiples n'utilise pas de statistique de test.
Interprétation
Minitab utilise la statistique de test pour calculer la valeur de p, qui vous permet de déterminer si des différences entre les écarts types sont significatives. La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Si la statistique de test est suffisamment élevée, la différence entre certains écarts types est statistiquement significative.
Vous pouvez utiliser la statistique de test afin de déterminer si l'hypothèse nulle doit être rejetée. Cependant, la valeur de p est plus souvent utilisée car elle est plus simple à interpréter.
Valeur de p
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Interprétation
Utilisez la valeur de p pour déterminer si certaines différences entre les écarts types sont statistiquement significatives. Minitab affiche les résultats d'un ou deux tests évaluant l'égalité des variances. Si vous disposez de deux valeurs de p non concordantes, reportez-vous à la rubrique "Tests".
Pour déterminer si des différences entre les écarts types sont statistiquement significatives, comparez la valeur de p à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle stipule que les moyennes de groupe sont toutes égales. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'une différence existe.
- Si la valeur de p est supérieure à α, les différences entre les écarts types ne sont pas statistiquement significatives.
- Si la valeur de p est inférieure ou égale à α, les différences entre certains écarts types sont statistiquement significatives.
Graphique récapitulatif
Le graphique récapitulatif affiche les valeurs de p et les intervalles de confiance pour les tests de l'égalité des variances. Les types de tests et d'intervalles affichés par Minitab dépendent de si vous avez sélectionné Utiliser le test en considérant une loi normale dans la boîte de dialogue Options, ainsi que du nombre de groupes dans vos données.
Si vous n'avez pas sélectionné Utiliser le test en considérant une loi normale, le graphique récapitulatif affiche les valeurs de p pour la méthode de comparaisons multiples et la méthode de Levene. Le graphique affiche également les intervalles de comparaisons multiples. Vous devez choisir entre les deux méthodes en fonction des propriétés de vos données.
Si vous avez sélectionné Utiliser le test en considérant une loi normale et que vous disposez de deux groupes, Minitab effectue un test F. Si vous disposez d'au moins 3 groupes, Minitab effectue un test de Bartlett. Dans les deux cas, le graphique indique aussi les intervalles de confiance de Bonferroni. Dans les deux cas, le graphique indique aussi les intervalles de confiance de Bonferroni.
Valeurs de p
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Utilisez les valeurs de p pour déterminer si certaines différences entre les écarts types sont statistiquement significatives. Minitab affiche les résultats d'un ou deux tests évaluant l'égalité des variances. Si vous disposez de deux valeurs de p non concordantes, reportez-vous à la section sur les tests pour savoir lequel utiliser.
Pour déterminer si des différences entre les écarts types sont statistiquement significatives, comparez la valeur de p à votre seuil de signification pour évaluer l'hypothèse nulle. L'hypothèse nulle stipule que les écarts types des groupes sont tous égaux. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'une différence existe.
- Si la valeur de p est supérieure à α, les différences entre les écarts types ne sont pas statistiquement significatives.
- Si la valeur de p est inférieure ou égale à α, les différences entre certains écarts types sont statistiquement significatives.
Les intervalles de comparaisons multiples
Si vous n'avez pas sélectionné Utiliser le test en considérant une loi normale, le graphique récapitulatif affiche les intervalles de comparaisons multiples.
Si la valeur de p du test de comparaisons multiples est valide pour votre étude, vous pouvez utiliser les intervalles de confiance de comparaisons multiples pour repérer des paires de groupes spécifiques présentant une différence statistiquement significative. Si deux intervalles ne se chevauchent pas, la différence entre les écarts types correspondants est statistiquement significative.
Si les propriétés de vos données vous obligent à utiliser la méthode de Levene, n'étudiez pas les intervalles de confiance du graphique récapitulatif.
Intervalles de confiance de Bonferroni
Si vous avez sélectionné Utiliser le test en considérant une loi normale, le graphique récapitulatif affiche les intervalles de confiance de Bonferroni.
Les intervalles de confiance de Bonferroni permettent d'estimer l'écart type de chaque population pour vos facteurs de catégorie. Chaque intervalle de confiance est une étendue de valeurs ayant de fortes chances de contenir l'écart type de la population correspondante. Minitab ajuste les intervalles de confiance de Bonferroni pour contrôler le niveau de confiance simultané.
Le contrôle du niveau de confiance simultané est particulièrement important lorsque vous évaluez plusieurs intervalles de confiance. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas l'écart type réel augmente avec le nombre d'intervalles de confiance.
Pour plus d'informations, reportez-vous aux rubriques Présentation des niveaux de confiance individuel et simultané dans les comparaisons multiples et Qu'est-ce que la méthode de Bonferroni ?
Remarque
Vous ne pouvez pas utiliser ces intervalles de confiance de Bonferroni pour déterminer si les différences entre des paires de groupes sont statistiquement significatives. Pour cela, vous devez utiliser les valeurs de p et les intervalles de confiance des comparaisons multiples du graphique récapitulatif.
Interprétation
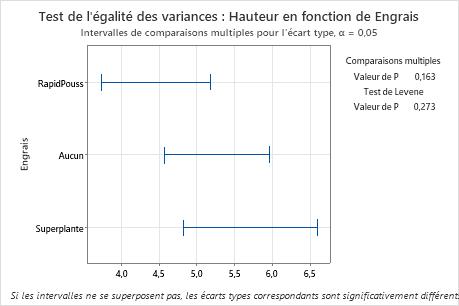
Dans ce graphique récapitulatif, la valeur de p pour le test des comparaisons multiples est supérieure au seuil de signification de 0,05. Aucune différence entre les groupes n'est statistiquement significative et tous les intervalles de comparaisons multiples se chevauchent.
Diagramme des valeurs individuelles
Un diagramme des valeurs individuelles présente les valeurs individuelles contenues dans chaque échantillon. Il facilite la comparaison des échantillons. Chaque cercle représente une observation. Le diagramme des valeurs individuelles est particulièrement utile lorsque l'effectif de votre échantillon est faible.
Interprétation
Utilisez un diagramme des valeurs individuelles pour examiner la dispersion des données et pour détecter d'éventuelles valeurs aberrantes. Les diagrammes des valeurs individuelles sont plus adaptés lorsque l'effectif d'échantillon est inférieur à 50.
- Données asymétriques
-
Examinez la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. Des données asymétriques indiquent qu'elles ne sont peut-être pas distribuées normalement. En général, l'asymétrie est plus facile à détecter avec un diagramme des valeurs individuelles, un histogramme ou une boîte à moustaches.
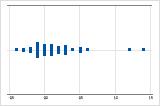
Asymétrie à droite
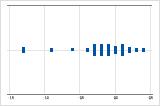
Asymétrie à gauche
Le diagramme des valeurs individuelles avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls quelques-uns sont plus longs. Le diagramme des valeurs individuelles avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments échouent immédiatement, une majorité échouent plus tard.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur vos résultats. En général, les valeurs aberrantes sont facilement identifiables sur un diagramme des valeurs individuelles.
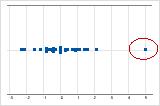
Sur un diagramme des valeurs individuelles, les valeurs de données anormalement élevées ou faibles indiquent de possibles valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
Boîte à moustaches
Une boîte a moustaches fournit un récapitulatif graphique de la loi de distribution de chaque échantillon. Elle facilite la comparaison de la forme, de la tendance centrale et de la variabilité des échantillons.
Interprétation
Utilisez une boîte à moustaches pour examiner la dispersion des données et pour détecter d'éventuelles valeurs aberrantes. Les boîtes à moustaches sont plus adaptées lorsque l'effectif d'échantillon est supérieur à 20.
- Données asymétriques
-
Examinez la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. Des données asymétriques indiquent qu'elles ne sont peut-être pas distribuées normalement. En général, l'asymétrie est plus facile à détecter avec un diagramme des valeurs individuelles, un histogramme ou une boîte à moustaches.
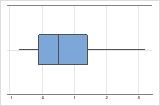
Asymétrie à droite
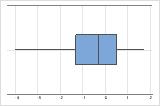
Asymétrie à gauche
La boîte à moustaches avec des données asymétriques à droite illustre des temps d'attente moyens. La plupart des temps d'attente sont relativement courts, seuls quelques-uns sont plus longs. La boîte à moustaches avec des données asymétriques à gauche représente des données de taux de défaillance. Quelques éléments échouent immédiatement, une majorité échouent plus tard.
Les données qui sont très asymétriques peuvent avoir une incidence sur la validité de la valeur de p si votre échantillon est petit (moins de 20 valeurs). Si vos données sont très asymétriques et que vous avez un petit échantillon, pensez éventuellement à augmenter l'effectif d'échantillon.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur vos résultats. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
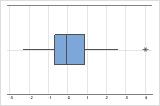
Sur une boîte à moustaches, les astérisques (*) indiquent les valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
