Notation
| Terme | Description |
|---|---|
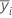 | moyenne d'échantillon pour l'ie niveau de facteur |
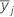 | moyenne d'échantillon pour le je niveau de facteur |
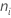 | nombre d'observations dans le niveau i |
| r | nombre de niveaux |
| s | écart type regroupé ou sqrt(MSE) |
| u | degrés de liberté pour l'erreur |
| α | probabilité simultanée de faire une erreur de 1ère espèce |
| α* | probabilité individuelle de faire une erreur de 1ère espèce |
Tukey :
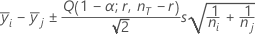
où Q = percentile α supérieur de la loi de l'étendue studentisée avec r et nT - r degrés de liberté.
Pour connaître le taux d'erreur individuel à partir du taux d'erreur simultané, utilisez la formule suivante :

Fisher :
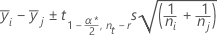
où t = point supérieur α/2 de la loi de Student avec u dl.
Pour connaître le niveau de confiance simultané à partir du taux d'erreur individuel, utilisez la formule suivante :

Dunnett :

Pour savoir comment est calculé d, reportez-vous à la page 63 dans Hsu1.
MCB de Hsu :
Nous proposons des formules pour les cas où tous les effectifs de groupes sont égaux à n. Les formules pour les effectifs de groupes inégaux sont disponibles dans Hsu1. Supposons que vous ayez choisi la moyenne la plus grande comme étant la plus adaptée et que vous souhaitiez obtenir l'intervalle de confiance pour l'ie moyenne moins la plus grande des autres moyennes.
La borne inférieure est la plus petite valeur entre zéro et

La borne supérieure est la plus grande valeur entre zéro et

Pour savoir comment est calculé d, reportez-vous à la page 83 dans Hsu1.
Lorsque la plus petite des moyennes de niveaux est la plus adaptée, les formules sont identiques, sauf que la valeur maximale est remplacée par la minimale.
Test de Welch et de Games-Howell
La statistique de test de Welch est calculée comme suit.
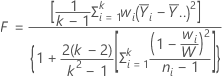
La valeur de p pour le test de Welch est une probabilité unilatérale à droite pour une loi F avec k - 1 comme degrés de liberté du numérateur, où k est le nombre de niveaux de X, et les degrés de liberté du dénominateur sont donnés par :
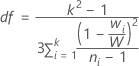
L'intervalle de comparaison pour μi - μj est
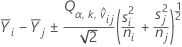
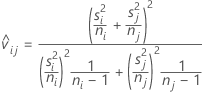
Le ratio t utilisé pour calculer la valeur de p ajustée est égal à :
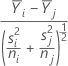
où :
la je réponse dans l'ie niveau du facteur de catégorie est égale à :Yij, j = 1, ...
La réponse moyenne de l'ie niveau est égale à :
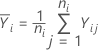
La variance d'échantillon est égale à :

La pondération pour le niveau i est égale à :
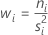
La somme de toutes les pondérations est égale à :
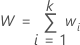
La moyenne pondérée globale des réponses est égale à :
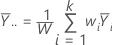
Remerciements
Nous remercions grandement Jason C. Hsu pour son aide quant à la conception et l'implémentation des comparaisons multiples.
[1] J.C. Hsu (1996). Multiple Comparisons, Theory and methods. Chapman & Hall.
