Sur ce thème
Notation
La notation est essentielle à la compréhension des modèles ANOVA. La notation utilisée pour l'analyse de variance à un facteur contrôlé est indiquée ci-dessous.
| Terme | Description |
|---|---|
| r | nombre de niveaux du facteur, i = 1 ...r |
| i | niveau de facteur donné |
| j | cas donné pour un niveau de facteur spécifique, j = 1 ...ni |
| yij | je observation de la réponse pour l'ie niveau de facteur |
| ni | nombre d'observations pour l'ie niveau de facteur |
| nT | nombre total de cas |
| μi | moyenne réelle des observations au ie niveau de facteur |
| yi. | nombre total d'observations au ie niveau de facteur |
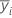 | moyenne de la réponse pour l'ie facteur |
Ajustement de modèles
Formule
Le modèle de l'analyse de variance à un facteur contrôlé peut être spécifié de différentes manières. Le modèle des moyennes des cellules est le suivant :
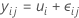
Toutes les observations du niveau de facteur ont la même prévision, μi. Etant donné que μi est une constante, toutes les observations ont la même variance, quel que soit le niveau de facteur.
Dans l'analyse de variance, l'estimation des moindres carrés est utilisée pour ajuster le modèle et générer des estimations pour les paramètres, μi.
Voici le test d'hypothèse pour l'analyse de variance à un facteur contrôlé :
H0 : μ1 = μ2= … = μr
H1 : au moins une moyenne n'est pas égale aux autres
Notation
| Terme | Description |
|---|---|
| μi | paramètres ou moyenne réelle des observations au ie niveau de facteur |
| εij | erreur indépendamment et normalement distribuée avec une moyenne de 0 et une variance constante de σ2 |
