Sélectionnez la méthode ou la formule de votre choix.
Moyenne
Formule
Moyenne des observations à un niveau de facteur donné.
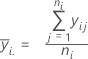
Notation
| Terme | Description |
|---|---|
| ni | nombre d'observations au niveau de facteur i |
| yij | valeur de la je observation au ie niveau de facteur |
Ecart type (EcTyp)
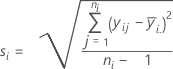
Notation
| Terme | Description |
|---|---|
| yij | observations au niveau de l'ie niveau de facteur |
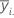 | moyenne des observations au ie niveau de facteur |
| ni | nombre d'observations au ie niveau de facteur |
Ecart type regroupé
Formule
Variance commune à toutes les observations. La variance regroupée est la suivante :
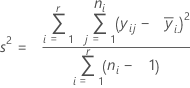
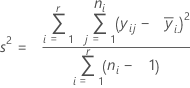
L'écart type regroupé est égal à la racine carrée de la formule précédente. En voici un équivalent :
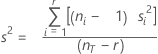
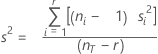
L'écart type regroupé est équivalent à S, qui se trouve dans les résultats et est égal à :

Notation
| Terme | Description |
|---|---|
| yij | je observation de la réponse pour l'ie niveau de facteur |
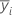 | moyenne de l'échantillon pour le niveau de facteur i |
| ni | nombre d'observations pour le ie niveau de facteur |
| nT | nombre total d'observations |
| si2 | variance des observations |
| r | nombre de niveaux du facteur |
| CM | Carré moyen |
Intervalles de confiance individuels
Formule
Les intervalles de confiance sont calculés pour chaque moyenne de niveau de facteur à l'aide de l'écart type regroupé. La formule est la suivante :
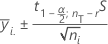
Notation
| Terme | Description |
|---|---|
| nT | nombre total d'observations |
| r | nombre de niveaux de facteurs |
| S | écart type regroupé |
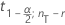 | fonction de la distribution cumulée inverse par rapport à la loi de Student à 1− α/2 avec nT − r degrés de liberté |
