Sur ce thème
- Etape 1 : Déterminer si les différences entre les moyennes des groupes sont statistiquement significatives
- Etape 2 : Etudier les moyennes des groupes
- Etape 3 : Comparer les moyennes de groupes
- Etape 4 : Déterminer l'ajustement du modèle aux données
- Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Etape 1 : Déterminer si les différences entre les moyennes des groupes sont statistiquement significatives
- Valeur de p ≤ α : les différences entre certaines moyennes sont statistiquement significatives.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et conclure que toutes les moyennes de population ne sont pas égales. Utilisez vos connaissances spécialisées afin de déterminer si les différences sont significatives dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Signification statistique et pratique.
- Valeur de p > α : les différences entre certaines moyennes ne sont pas statistiquement significatives.
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle car vous n'êtes pas en mesure de conclure que les moyennes de population sont égales. Vérifiez que le test est assez puissant pour détecter une différence qui est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Augmenter la puissance d'un test d'hypothèse.
Analyse de la variance
| Source | DL | SomCar ajust | CM ajust | Valeur F | Valeur de p |
|---|---|---|---|---|---|
| Peinture | 3 | 281,7 | 93,90 | 6,02 | 0,004 |
| Erreur | 20 | 312,1 | 15,60 | ||
| Total | 23 | 593,8 |
Résultat principal : valeur de p
Dans ces résultats, l'hypothèse nulle stipule que les valeurs de dureté moyenne de 4 peintures différentes sont égales. La valeur de p étant inférieure au seuil de signification de 0,05, vous pouvez rejeter l'hypothèse nulle et conclure que certaines peintures ont des moyennes différentes.
Etape 2 : Etudier les moyennes des groupes
Utilisez le graphique des intervalles pour afficher la moyenne et l'intervalle de confiance pour chaque groupe.
- Chaque point représente une moyenne d'échantillon.
- Chaque intervalle est un intervalle de confiance à 95 % pour la moyenne d'un groupe. Vous pouvez être sûr à 95 % qu'une moyenne de groupe est comprise dans l'intervalle de confiance du groupe.
Important
Ces intervalles sont néanmoins à interpréter avec prudence, car le taux d'erreur de 1ère espèce augmente lorsque vous effectuez des comparaisons multiples. En d'autres termes, lorsque vous augmentez le nombre de comparaisons, vous augmentez également la probabilité qu'au moins une comparaison conclue à tort que l'une des différences observées est significativement différente.
Pour évaluer les différences qui apparaissent sur ce graphique, utilisez le tableau d'informations de groupement et d'autres résultats de comparaisons (décrit à l'étape 3).
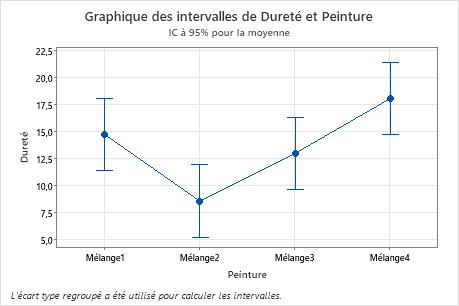
Dans le graphique des intervalles, le mélange 2 présente la moyenne la plus faible, et le mélange 4 la plus élevée. Ce graphique ne vous permet pas de déterminer si ces différences sont significatives. Pour évaluer l'importance statistique, examinez les intervalles de confiance des différences entre les moyennes.
Etape 3 : Comparer les moyennes de groupes
Si la valeur de p de votre ANOVA à un facteur contrôlé est inférieure au seuil de signification, cela signifie que certaines des moyennes de groupes sont différentes, mais vous ne pouvez pas savoir quelles paires de groupes. Utilisez le tableau d'informations de groupement et les tests pour les différences de moyennes afin de déterminer si la différence moyenne entre des paires spécifiques de groupes est statistiquement significative et d'évaluer l'importance de la différence.
Pour plus d'informations sur les méthodes de comparaison, reportez-vous à Utilisation de comparaisons multiples pour évaluer la signification pratique et statistique.
- Tableau d'informations de groupement
-
Utilisez le tableau d'informations de groupement pour déterminer rapidement si la différence moyenne entre toute paire de groupes est statistiquement significative.
Les groupes qui n'ont aucune lettre en commun présentent une différence significative.
- Tests relatifs aux différences de moyennes
-
Utilisez les intervalles de confiance afin de déterminer les étendues de valeurs probables pour les différences et de déterminer si les différences sont significatives sur le plan concret. Le tableau présente un ensemble d'intervalles de confiance pour la différence entre des paires de moyennes. Le graphique des intervalles relatif aux différences de moyennes présente les mêmes informations.
Les intervalles de confiance qui ne contiennent pas la valeur zéro indiquent une différence moyenne qui est statistiquement significative.
En fonction de la méthode de comparaison choisie, le tableau compare différentes paires de groupes et affiche l'un des types d'intervalles de confiance suivants.-
Niveau de confiance individuel
Pourcentage d'occurrences, dans un même intervalle de confiance, de la différence réelle entre une paire de moyennes de groupes, si l'étude est répétée plusieurs fois.
-
Niveau de confiance simultané
Pourcentage d'occurrences, dans un ensemble d'intervalles de confiance, des différences réelles pour toutes les comparaisons de groupes, si l'étude est répétée plusieurs fois.
Le contrôle du niveau de confiance simultané est particulièrement important lorsque vous réalisez plusieurs comparaisons. Si vous ne le contrôlez pas, la probabilité qu'au moins un intervalle de confiance ne contienne pas la différence réelle augmente avec le nombre de comparaisons.
-
Pour plus d'informations, reportez-vous à la rubrique Présentation des niveaux de confiance individuel et simultané dans les comparaisons multiples.
Pour plus d'informations sur la manière d'interpréter les résultats des MCB de Hsu, reportez-vous à Qu'est-ce que la méthode de comparaisons multiples avec le meilleur (MCB) niveau de Hsu ?.
Informations de groupement avec la méthode de Tukey et un niveau de confiance de 95 %
| Peinture | N | Moyenne | Groupement | |
|---|---|---|---|---|
| Mélange4 | 6 | 18,07 | A | |
| Mélange1 | 6 | 14,73 | A | B |
| Mélange3 | 6 | 12,98 | A | B |
| Mélange2 | 6 | 8,57 | B | |
Résultats principaux : Moyenne, Groupement
Dans ces résultats, le tableau montre que le groupe A contient les mélanges 1, 3 et 4, et que le groupe B contient les mélanges 1, 2 et 3. Les mélanges 1 et 3 sont dans les deux groupes. Les différences entre les moyennes qui partagent une lettre ne sont pas statistiquement significatives. Les mélanges 2 et 4 ne partagent pas de lettre, ce qui indique que la moyenne du mélange 4 est bien plus élevée que celle du mélange 2.
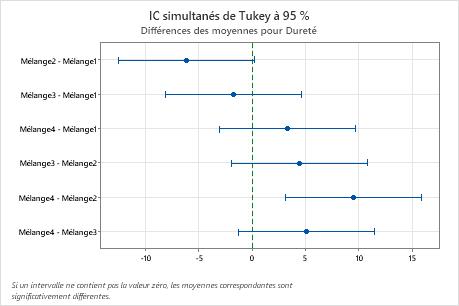
Tests de simultanéité de Tukey pour les différences des moyennes
| Différence des niveaux | Différence des moyennes | Erreur type de la différence | IC à 95 % | Valeur de T | Valeur de p ajustée |
|---|---|---|---|---|---|
| Mélange2 - Mélange1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mélange3 - Mélange1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mélange4 - Mélange1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mélange3 - Mélange2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mélange4 - Mélange2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mélange4 - Mélange3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
Résultats principaux : IC simultanés à 95 %, niveau de confiance individuel
- L'intervalle de confiance pour la différence entre les moyennes des mélanges 2 et 4 s'étend de 3,11 à 15,89. Cette étendue ne comprend pas la valeur zéro, ce qui indique que la différence est statistiquement significative.
- Les intervalles de confiance pour les paires de moyennes restantes comprennent tous la valeur zéro, ce qui indique que les différences ne sont pas statistiquement significatives.
- Le niveau de confiance simultané à 95 % indique que vous pouvez être sûr à 95 % que tous les intervalles de confiance contiennent les différences réelles.
- Le tableau indique que le niveau de confiance individuel est de 98,89 %. Ce résultat indique que vous pouvez être sûr à 98,89 % que chaque intervalle individuel contient la différence réelle dans une paire spécifique de moyennes de groupes. Les niveaux de confiance individuels pour chaque comparaison génèrent le niveau de confiance simultané à 95 % pour les six comparaisons.
Etape 4 : Déterminer l'ajustement du modèle aux données
Pour déterminer l'ajustement du modèle aux données, étudiez les statistiques d'adéquation de l'ajustement dans le tableau Récapitulatif du modèle.
- S
- Utilisez S pour évaluer la capacité du modèle à décrire la réponse.
S est mesuré en unités de la variable de réponse et représente la distance entre les valeurs de données et les valeurs ajustées. Plus S est petit, mieux le modèle décrit la réponse. Cependant, une faible valeur de S n'indique pas en soi que le modèle respecte les hypothèses du modèle. Vous devez examiner les graphiques des valeurs résiduelles pour vérifier les hypothèses.
- R carré
-
R2 représente le pourcentage de variation de la réponse expliqué par le modèle. Plus la valeur R2 est élevée, plus le modèle est ajusté à vos données. R2 est toujours compris entre 0 et 100 %.
Une valeur élevée de R2 n'indique pas que le modèle vérifie les hypothèses. Vous devez examiner les graphiques des valeurs résiduelles pour vérifier les hypothèses.
- R carré (prév)
-
La valeur R2 prévu permet de déterminer la capacité de votre modèle à prévoir la réponse pour de nouvelles observations.Les modèles ayant des valeurs de R2 prévu élevées ont une meilleure capacité de prévision.
Une valeur de R2 prévu considérablement inférieure à R2 peut être un signe de surajustement du modèle. Un modèle est dit surajusté lorsqu'il inclut des termes pour des effets qui ne sont pas importants dans la population. Le modèle est alors spécialement ajusté aux données des échantillons, mais risque ne pas être utile pour effectuer des prévisions concernant la population entière.
La valeur R2 prévu peut également être plus utile que R2 ajusté pour comparer des modèles, car elle est calculée avec des observations qui ne sont pas incluses dans le calcul du modèle.
Récapitulatif du modèle
| S | R carré | R carré (ajust) | R carré (prév) |
|---|---|---|---|
| 3,95012 | 47,44% | 39,56% | 24,32% |
Résultats principaux : S, R carré, R carré (prév)
Dans ces résultats, le facteur explique 47,44 % de la variation dans la réponse. S indique que l'écart type entre les points de données et les valeurs ajustées est d'environ 3,95 unités.
Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
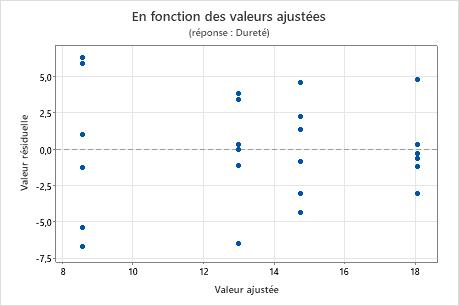
Graphique des valeurs résiduelles en fonction des valeurs ajustées
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Un point très éloigné de zéro | Une valeur aberrante |
Graphique des valeurs résiduelles en fonction de l'ordre
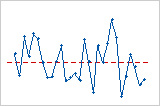
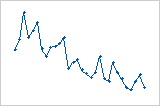
Tendance
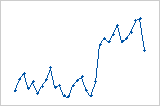
Equipe
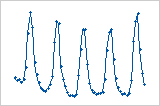
Cycle
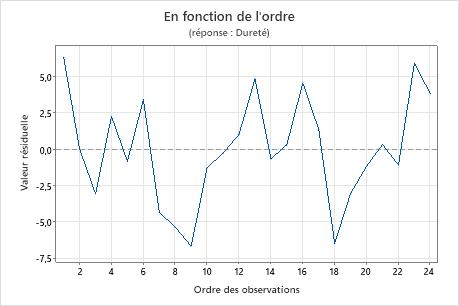
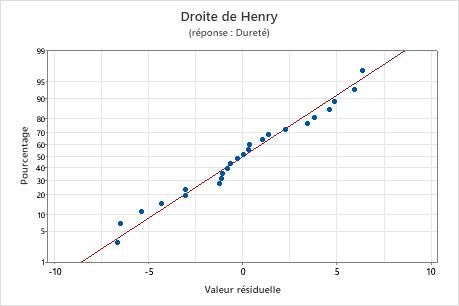
Droite de Henry des valeurs résiduelles
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
| Schéma | Ce que le schéma indique |
|---|---|
| Une ligne qui n'est pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Une modification de la pente | Une variable non identifiée |
Remarque
Si votre plan d'ANOVA à un facteur contrôlé suit les règles pour les effectifs d'échantillon, les écarts par rapport à la normalité n'ont pas d'impact considérable sur les résultats.