Un ingénieur chimiste cherche à comparer la dureté de quatre mélanges de peintures. Six échantillons de chaque mélange de peinture ont été appliqués sur un morceau de métal. Les morceaux de métal ont été passés au four. Ensuite, la dureté de chaque échantillon a ensuite été mesurée. Pour tester l'égalité des moyennes et évaluer les différences entre les paires de moyennes, l'analyste utilise l'ANOVA à un facteur contrôlé avec des comparaisons multiples.
- Ouvrez le fichier de données échantillons, DuretéPeinture.MWX.
- Sélectionnez .
- Sélectionnez Les données de réponse se trouvent dans une colonne pour tous les niveaux de facteurs.
- Dans la zone Réponse, saisissez Dureté.
- Dans la zone Facteur, saisissez Peinture.
- Cliquez sur le bouton Comparaisons, puis sélectionnez Tukey.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
La valeur de p dans l'ANOVA pour la dureté de la peinture est inférieure à 0,05. Ce résultat indique que la dureté des mélanges de peintures diffère de manière significative. L'ingénieur sait que certaines moyennes de groupes sont différentes.
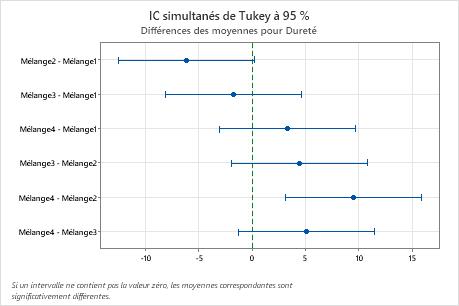
L'ingénieur utilise les résultats de la comparaison de Tukey pour effectuer un test formel permettant de déterminer si la différence entre une paire de groupes est statistiquement significative. Le graphique qui inclut les intervalles de confiance simultanés de Tukey montre que l'intervalle de confiance pour la différence entre les moyennes des mélanges 2 et 4 s'étend de 3,114 à 15,886. Cette étendue ne comprend pas la valeur zéro, ce qui indique que la différence entre ces moyennes est significative. L'ingénieur peut utiliser cette estimation de la différence pour déterminer si la différence est significative sur le plan concret.
Les intervalles de confiance pour les paires de moyennes restantes comprennent tous la valeur zéro, ce qui indique que les différences ne sont pas significatives.
La faible valeur de R2 prévue (24,32 %) indique que le modèle génère des prévisions imprécises pour de nouvelles observations. Cette imprécision peut être due à la petite taille de l'effectif des groupes. Par conséquent, l'ingénieur ne doit pas utiliser le modèle pour faire des généralisations au-delà des données échantillons.
Méthode
| Hypothèse nulle | Toutes les moyennes sont égales |
|---|---|
| Hypothèse alternative | Toutes les moyenne ne sont pas égales |
| Seuil de signification | α = 0,05 |
Informations sur les facteurs
| Facteur | Niveaux | Valeurs |
|---|---|---|
| Peinture | 4 | Mélange1; Mélange2; Mélange3; Mélange4 |
Analyse de la variance
| Source | DL | SomCar ajust | CM ajust | Valeur F | Valeur de p |
|---|---|---|---|---|---|
| Peinture | 3 | 281,7 | 93,90 | 6,02 | 0,004 |
| Erreur | 20 | 312,1 | 15,60 | ||
| Total | 23 | 593,8 |
Récapitulatif du modèle
| S | R carré | R carré (ajust) | R carré (prév) |
|---|---|---|---|
| 3,95012 | 47,44% | 39,56% | 24,32% |
Moyennes
| Peinture | N | Moyenne | EcTyp | IC à 95 % |
|---|---|---|---|---|
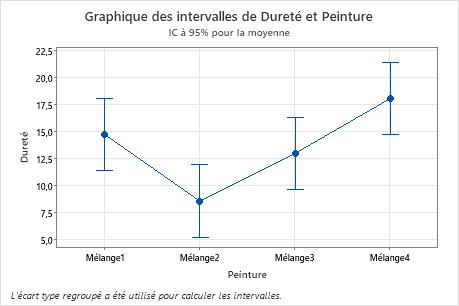
| Mélange1 | 6 | 14,73 | 3,36 | (11,37; 18,10) |
| Mélange2 | 6 | 8,57 | 5,50 | (5,20; 11,93) |
| Mélange3 | 6 | 12,98 | 3,73 | (9,62; 16,35) |
| Mélange4 | 6 | 18,07 | 2,64 | (14,70; 21,43) |
Informations de groupement avec la méthode de Tukey et un niveau de confiance de 95 %
| Peinture | N | Moyenne | Groupement | |
|---|---|---|---|---|
| Mélange4 | 6 | 18,07 | A | |
| Mélange1 | 6 | 14,73 | A | B |
| Mélange3 | 6 | 12,98 | A | B |
| Mélange2 | 6 | 8,57 | B | |