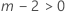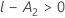Sur ce thème
Tests des termes d'effet fixe
Les tests des termes d'effet fixe sont des tests F. L'hypothèse nulle du test change selon qu'il porte sur un facteur fixe ou sur une covariable. Pour un facteur fixe, l'hypothèse nulle est que le terme n'a pas d'influence significative sur la réponse. Pour une covariable, l'hypothèse nulle est qu'il n'existe aucune association entre la covariable et la réponse.
Minitab propose les deux méthodes suivantes afin de tester les termes d'effet fixe : l'approximation de Kenward-Roger et l'approximation de Satterthwaite. Pour plus d'informations sur l'approximation de Kenward-Roger, reportez-vous à Kenward et Roger.1 Pour plus d'informations sur l'approximation de Satterthwaite, reportez-vous à Giesbrecht et Burns 2, ainsi qu'à Fai et Cornelius. 3.
Le calcul des degrés de liberté du dénominateur pour la statistique F et le calcul de la statistique F sont différents. Le calcul des degrés de liberté du numérateur et la méthode permettant de déterminer une valeur de p pour une statistique F donnée sont identiques pour les deux méthodes.
Approximation de Kenward-Roger
L'approximation de Kenward-Roger est une méthode permettant de tester la signification statistique des termes d'effet fixe.
Statistique F
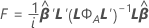
où
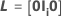
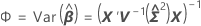
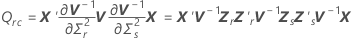
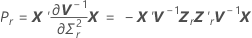
Notation
| Terme | Description |
|---|---|
| l | degrés de liberté du numérateur, qui correspondent au nombre de paramètres dans le terme à tester |
| 0 | matrice avec 0 composante |
| Il | matrice d'identité de dimension l |
| c + 1 | nombre de composantes de la variance |
| wrs | (r, s)e composante de la matrice de variance/covariance asymptotique de  |
| V−1 | inverse de la matrice de variance/covariance |
Pour plus de détails sur la notation, reportez-vous à la rubrique sur les méthodes.
Degrés de liberté du dénominateur
où
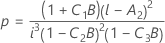
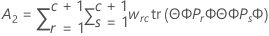
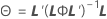
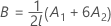
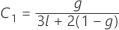
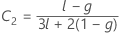
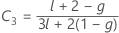
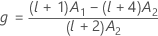
λ de Kenward et Roger
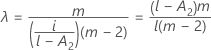
Si l'une des conditions n'est pas vérifiée, λ = 1.
Sous l'hypothèse nulle, lambda × F suit la loi F asymptotiquement avec les degrés de liberté DL Numérateur et DL Dénominateur. Le calcul de la valeur de p utilise cette propriété.
Approximation de Satterthwaite
L'approximation de Satterthwaite est une méthode permettant de tester la signification statistique des termes d'effet fixe.
Statistique F
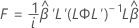
où L et 
ont les mêmes définitions que pour l'approximation de Kenward-Roger.
Degrés de liberté du dénominateur
Le procédé visant à déterminer les degrés de liberté comporte plusieurs étapes.
-
Effectuez une décomposition spectrale de la variance de l'estimation de vecteur du paramètre des effets fixes, comme indiqué ci-dessous :
où P est une matrice orthogonale des valeurs propres et D est une matrice diagonale des valeurs propres, toutes deux de dimension l × l.
-
Définissez lr comme la re ligne de P'L, r = 1, ..., l, soit
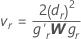où dr correspond au re élément de la diagonale de D, où W est la matrice de variance/covariance asymptotique de
et gr est le vecteur de gradient des éléments suivants :
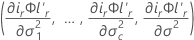
où
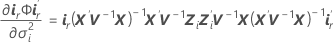
i = 1, …, c, et
-
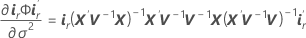
Soit
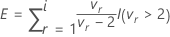
où
est une fonction indicatrice éliminant des termes avec 
-
Les degrés de liberté du dénominateur dépendent de la valeur de E.
- Si E > l, les degrés de liberté sont calculés comme suit :
- Sinon, DL Dénominateur = 1
- Si E > l, les degrés de liberté sont calculés comme suit :
Degrés de liberté du numérateur (DL Numérateur)
| Effet | DL |
|---|---|
| Facteur fixe |  |
| Covariable | 1 |
| Interactions impliquant des facteurs fixes |  |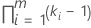
Notation
| Terme | Description |
|---|---|
| k | nombre de niveaux du facteur fixe |
| m | nombre de facteurs dans l'interaction |
Valeur de p - Tests des effets fixes
Notation
| Terme | Description |
|---|---|
 | fonction de répartition de la loi F avec un nombre de degrés de liberté respectivement égal à DL Numérateur et DL Dénominateur |
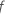 | valeur F calculée pour un terme |
