Sur ce thème
Modèle à effets mixtes et log de vraisemblance
Forme générale du modèle à effets mixtes
Les modèles à effets mixtes contiennent des effets fixes et aléatoires. La forme générale du modèle à effets mixtes est la suivante :
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
Notation
| Terme | Description |
|---|---|
| y | vecteur n x 1 des valeurs de réponse |
| X | matrice de plan n x p pour les termes d'effet fixe, p ≤ n |
| β | vecteur p x 1 de paramètres inconnus |
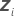 | matrice de plan n x mi pour l' terme aléatoire dans le modèle terme aléatoire dans le modèle |
| μi | vecteur mi x 1 de variables indépendantes issues d'une loi N(0,  ) ) |
| ε | vecteur n x 1 de variables indépendantes issues d'une loi N(0,  ) ) |
| n | nombre d'observations |
| p | nombre de paramètres dans  |
| c | nombre de termes aléatoires dans le modèle |
Matrice de variance/covariance
D'après l'hypothèse pour la forme générale du modèle à effets mixtes, le vecteur de réponse, y, suit une loi normale multivariée ayant pour vecteur moyen Xβ et la matrice de variance/covariance suivante :
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
où
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c sont appelés des composantes de la variance.
En factorisant la variance, vous pouvez trouver une représentation de H(θ), qui se trouve dans le calcul du log de vraisemblance des modèles à effets mixtes.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
Notation
| Terme | Description |
|---|---|
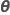 | 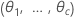 |
| θi | 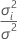 rapport de la variance de l' rapport de la variance de l' terme aléatoire par rapport à la variance d'erreur terme aléatoire par rapport à la variance d'erreur |
Log de vraisemblance


Notation
| Terme | Description |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | déterminant de H |
| H-1 | inverse de H |
| mi | nombre de niveaux pour l' terme aléatoire terme aléatoire |
 | composante de variance pour l'erreur |
| In | matrice d'identité avec n lignes et colonnes |
Estimation par le maximum de vraisemblance restreinte (REML)
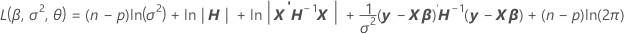
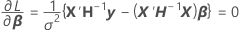
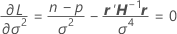
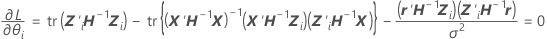
où 
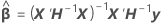
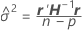
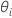 ne peut pas être résolue de manière explicite pour
ne peut pas être résolue de manière explicite pour 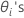 . Minitab utilise la méthode de Newton pour estimer
. Minitab utilise la méthode de Newton pour estimer 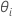 en suivant la procédure ci-dessous :
en suivant la procédure ci-dessous :
- Utilisez les estimations MINQUE12 des composantes de la variance afin de définir les valeurs initiales de σ2 et de θi.
- Estimez β et σ2 avec les équations pour
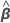 et
et 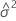 .
. - Recherchez la valeur de θi à l'aide de la méthode de Newton afin de minimiser L(β, σ2, θ).
- Reproduisez les étapes 2 et 3 jusqu'à convergence.
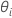 correspondent aux estimations du rapport des variances. La composante de variance pour l'
correspondent aux estimations du rapport des variances. La composante de variance pour l' terme aléatoire est calculée comme suit :
terme aléatoire est calculée comme suit :

Notation
| Terme | Description |
|---|---|
| tr(·) | trace de la matrice |
| X' | transposition de X |
