Sur ce thème
Ajustement marginal
Les ajustements marginaux représentent les réponses moyennes à différents niveaux de facteurs fixes. Les ajustements marginaux sont calculés à partir des équations ajustées marginales.
ErT ajust
L'erreur type de l'ajustement (ErT ajust) estime la variation de la réponse moyenne estimée pour les valeurs de variables spécifiées. Le calcul de l'intervalle de confiance de la réponse moyenne utilise l'erreur type de la valeur ajustée. Les erreurs types ne sont jamais négatives.
DL pour la moyenne marginale
Les degrés de liberté (DL) représentent la quantité d'informations disponible dans les données pour estimer l'intervalle de confiance pour la réponse moyenne.
Interprétation
Utilisez les DL pour comparer la quantité d'informations disponible sur les différentes moyennes marginales. Généralement, plus le nombre de degrés de liberté est élevé, plus l'intervalle de confiance pour la moyenne est étroit. Les erreurs types étant différentes selon les observations, l'intervalle de confiance d'une moyenne ayant un nombre plus important de degrés de liberté n'est pas forcément plus étroit que celui d'une moyenne ayant moins de degrés de liberté.
Intervalle de confiance de la moyenne marginale (IC à 95 %)
Ces intervalles de confiance (IC) sont des étendues de valeurs ayant de fortes chances de contenir les réponses moyennes marginales correspondantes.
Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Cependant, si vous prélevez de nombreux échantillons, un certain pourcentage des intervalles de confiance obtenus contiendra le paramètre de population inconnu. Le pourcentage de ces intervalles de confiance contenant le paramètre est le niveau de confiance de l'intervalle.
L'intervalle de confiance est composé de deux parties :
Interprétation
Les intervalles de confiance permettent d'évaluer si les réponses moyennes marginales sont statistiquement supérieures, inférieures ou égales à une valeur spécifique. Vous pouvez également utiliser les intervalles de confiance pour déterminer une étendue de valeurs pour les réponses moyennes marginales inconnues correspondantes.
Valeur résiduelle marginale
Une valeur résiduelle (ei) est la différence entre une valeur observée (y) et la valeur ajustée marginale correspondante, (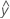 ).
).
Interprétation
Créez un graphique des valeurs résiduelles pour déterminer si votre modèle est adapté et si les hypothèses de modèle à effets mixtes sont satisfaites. L'examen des valeurs résiduelles peut fournir des informations utiles sur l'ajustement du modèle aux données. De manière générale, les valeurs résiduelles doivent être distribuées de manière aléatoire sans aucun schéma clair ni aucune valeur aberrante. Si Minitab détermine que vos données comprennent des observations aberrantes, il les indique dans les résultats, dans le tableau Ajustements et diagnostics marginaux pour les observations aberrantes. Les observations aberrantes signalées par Minitab suivent mal l'équation marginale proposée. Toutefois, il est normal d'obtenir quelques observations aberrantes. Par exemple, en vous fondant sur les critères de valeurs résiduelles élevées, vous pouvez vous attendre à ce qu'environ 5 % de vos observations soient signalées pour leur valeur résiduelle importante.
Val. résid. norm
La valeur résiduelle marginale normalisée est égale à la valeur résiduelle (ei) divisée par une estimation de son écart type.
Interprétation
Utilisez les valeurs résiduelles marginales normalisées pour détecter les valeurs aberrantes. Les valeurs résiduelles marginales normalisées supérieures à 2 et inférieures à −2 sont généralement considérées comme élevées. Le tableau Ajustements et diagnostics marginaux conditionnels pour les observations aberrantes signale ces observations avec un "R". Les observations signalées par Minitab suivent mal l'équation ajustée marginale proposée. Toutefois, il est normal d'obtenir quelques observations aberrantes. Par exemple, selon les critères utilisés pour définir des valeurs résiduelles marginales normalisées élevées, vous pouvez vous attendre à ce qu'environ 5 % de vos observations soient signalées pour leur valeur résiduelle normalisée importante.
Les valeurs résiduelles marginales normalisées sont utiles, car les valeurs résiduelles marginales brutes ne permettent pas toujours de détecter les valeurs aberrantes. La variance de chaque valeur résiduelle marginale brute peut être différente en fonction des valeurs X qui lui sont associées. Cette variation inégale complique l'évaluation de la grandeur des valeurs résiduelles marginales brutes. La normalisation des valeurs résiduelles marginales résout ce problème en transformant les différentes variances selon une échelle commune.
Hi (effet de levier)
Les valeurs Hi dans un modèle à effets mixtes peuvent être utilisées afin d'identifier les points de données dont les paramètres d'effet de levier sont élevés uniquement pour les termes d'effet fixe. La matrice de plan utilisée pour calculer les valeurs Hi est la matrice de plan des termes d'effet fixe.
Interprétation
Les valeurs Hi sont comprises entre 0 et 1. Dans le tableau Ajustements et diagnostics marginaux pour les observations aberrantes, Minitab affecte un X aux observations qui présentent soit un effet de levier supérieur à 3p/n, soit à la valeur 0,99, en considérant en priorité la plus petite de ces valeurs. Dans la valeur 3p/n, p représente le nombre de coefficients du modèle et n le nombre d'observations. Les observations que Minitab signale par un "X" peuvent être influentes.
Les observations influentes ont un effet disproportionné sur le modèle et peuvent générer des résultats trompeurs. Par exemple, un coefficient pourra être statistiquement significatif ou non selon qu'un point influent est inclus ou exclus. Les observations influentes peuvent être des points à effet de levier et/ou des valeurs aberrantes.
En cas d'observation influente, déterminez si elle est due à une erreur d'entrée de données ou de mesure. Si l'observation n'est due ni à une erreur d'entrée de données, ni à une erreur de mesure, déterminez dans quelle mesure l'observation est influente. Tout d'abord, ajustez le modèle avec et sans observation. Ensuite, comparez les coefficients, les valeurs de p, le R2, et d'autres informations relatives au modèle. Si le modèle change de manière significative lorsque vous supprimez l'observation influente, examinez le modèle plus en détail pour déterminer si vous avez spécifié le modèle de façon incorrecte. Vous pouvez être amené à rassembler davantage de données pour résoudre le problème.
