Un chercheur teste les rendements de six variétés de luzerne sur quatre terrains choisis aléatoirement. Le rendement de chaque variété a été enregistré pour chaque terrain.
Le chercheur souhaite savoir si la variété de la luzerne influe sur le rendement moyen. Il dispose de 4 terrains où collecter les données. Cependant, il souhaite modéliser la manière dont pousse la luzerne sur des terrains qui ne sont pas pris en compte dans l'expérience. C'est pourquoi il décide que le terrain où pousse la luzerne est un facteur aléatoire. Il utilise un modèle à effets mixtes pour évaluer à la fois les effets fixes et les effets aléatoires.
- Ouvrez le fichier de données échantillons, Alfalfa.MWX.
- Sélectionnez .
- Dans la zone Réponses , saisissez Rendement.
- Dans la zone Facteurs aléatoires (obligatoires) , saisissez Terrain.
- Dans la zone Facteurs fixes , saisissez Variété.
- Cliquez sur Graphiques.
- Dans Valeurs résiduelles des graphiques , sélectionnez Conditionnel, normalisé.
- Dans Graphiques des valeurs résiduelles, sélectionnez Quatre en un.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
Dans le tableau des composantes de la variance, la valeur de p pour Terrain est égale à 0,124. Le test d'hypothèse ne permet pas de prouver que la composante de la variance est différente de 0. La valeur de p de la composante de variance pour l'erreur est 0,003. Sachant que la valeur de p est inférieure au seuil de signification de 0,05, le chercheur peut conclure que la composante de variance pour l'erreur n'est pas égale à 0.
La valeur de p d'environ 0 pour le facteur fixe, Variété, indique qu'au moins un type de luzerne a un effet sur le rendement significativement différent des cinq autres types.
Les coefficients des effets principaux représentent la différence entre chaque moyenne de niveau et la moyenne générale. Par exemple, le facteur Variété 1 est associé à un rendement de la luzerne d'environ 0,385 unité de plus que la moyenne générale. La valeur de p d'environ 0 pour ce coefficient indique que l'effet de Variété 1 sur le rendement est significativement différent de l'effet d'un autre niveau du terme Variété. Pour déterminer les effets de niveaux qui sont statistiquement égaux et ceux qui sont statistiquement différents, le chercheur envisage d'effectuer une analyse de comparaisons multiples pour le terme.
La valeur R2 indique que le modèle explique environ 92 % de la variation du rendement. La valeur R carré (ajust) aussi est élevée, avec environ 90,2 %. Le chercheur utilise cette valeur pour comparer des modèles ayant un nombre de prédicteurs différent.
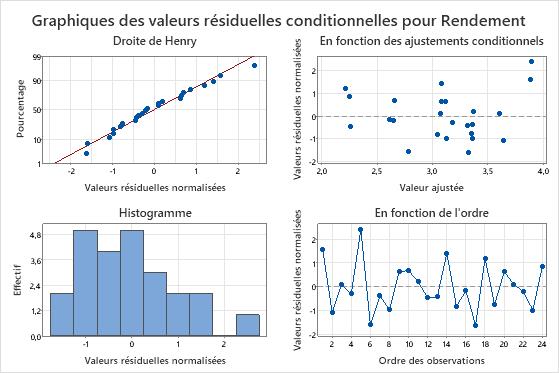
Les observations 1 et 5 sont aberrantes car elles contiennent des valeurs résiduelles normalisées supérieures à 2. Le chercheur examine les données pour vérifier que les valeurs de réponse pour ces observations sont correctes.
Les valeurs résiduelles sur la droite de Henry se rapprochent d'une ligne droite et les points semblent être répartis aléatoirement autour de 0 sur le diagramme des valeurs résiduelles en fonction des valeurs ajustées.
Méthode
| Estimation de la variance | Maximum de vraisemblance restreint |
|---|---|
| DL pour effets fixes | Kenward-Roger |
Informations sur les facteurs
| Facteur | Type | Niveaux | Valeurs |
|---|---|---|---|
| Terrain | Aléatoire | 4 | 1; 2; 3; 4 |
| Variété | Fixe | 6 | 1; 2; 3; 4; 5; 6 |
Composantes de la variance
| Source | Var | % du total | Var. ErT | Valeur de Z | Valeur de p |
|---|---|---|---|---|---|
| Terrain | 0,077919 | 72,93% | 0,067580 | 1,152996 | 0,124 |
| Erreur | 0,028924 | 27,07% | 0,010562 | 2,738613 | 0,003 |
| Total | 0,106843 |
Tests pour effets fixes
| Terme | DL Num | DL Dén | Valeur F | Valeur de p |
|---|---|---|---|---|
| Variété | 5,00 | 15,00 | 26,29 | 0,000 |
Récapitulatif du modèle
| S | R carré | R carré (ajust) | AICc | BIC |
|---|---|---|---|---|
| 0,170071 | 92,33% | 90,20% | 12,54 | 13,52 |
Coefficients
| Terme | Coeff | Coef ErT | DL | Valeur de T | Valeur de p |
|---|---|---|---|---|---|
| Constante | 3,094583 | 0,143822 | 3,00 | 21,516692 | 0,000 |
| Variété | |||||
| 1 | 0,385417 | 0,077626 | 15,00 | 4,965016 | 0,000 |
| 2 | 0,145417 | 0,077626 | 15,00 | 1,873287 | 0,081 |
| 3 | 0,107917 | 0,077626 | 15,00 | 1,390205 | 0,185 |
| 4 | -0,319583 | 0,077626 | 15,00 | -4,116938 | 0,001 |
| 5 | 0,395417 | 0,077626 | 15,00 | 5,093838 | 0,000 |
Ajustements et diagnostics marginaux pour les observations aberrantes
| Observation | Rendement | Valeur ajustée | Résiduelle | Val. résid. norm. | |
|---|---|---|---|---|---|
| 1 | 4,100000 | 3,480000 | 0,620000 | 2,190221 | R |
| 5 | 4,220000 | 3,490000 | 0,730000 | 2,578808 | R |
Ajustements et diagnostics conditionnels pour les observations aberrantes
| Observation | Rendement | Valeur ajustée | Résiduelle | Val. résid. norm. | |
|---|---|---|---|---|---|
| 5 | 4,220000 | 3,895339 | 0,324661 | 2,400733 | R |