Un ingénieur souhaite évaluer l'effet du temps de frittage sur la résistance à la compression de trois métaux différents. L'ingénieur mesure la résistance de cinq échantillons de chaque type de métal pour chaque temps de frittage : 100 minutes, 150 minutes et 200 minutes.
L'ingénieur effectue une ANOVA avec un modèle linéaire général (MLG) et ajoute un diagramme des interactions aux résultats.
- Ouvrez le fichier de données échantillons, TempsFrittage.MWX.
- Sélectionnez .
- Dans la zone Réponses, saisissez Résistance.
- Dans la zone Facteurs, saisissez TempsFrittage et TypeMétal.
- Cliquez sur OK.
Interprétation des résultats
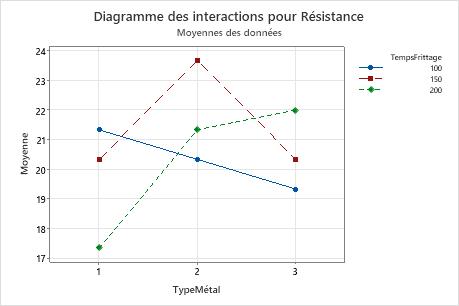
Le diagramme des interactions indique la résistance moyenne en fonction du temps de frittage pour les trois types de métal. Les droites non parallèles sur le diagramme des interactions représentent les effets d'interaction entre un type de métal et le temps de frittage. Cet effet d'interaction indique que la relation entre le type de métal et la résistance dépend du temps de frittage.
Si l'ingénieur utilise TypeMétal 2, TempsFrittage 150 est associé à la résistance moyenne la plus élevée. En revanche, si l'ingénieur utilise TypeMétal 1, c'est la valeur TempsFrittage 100 qui est associée à la résistance moyenne la plus haute.
Bien que vous puissiez utiliser ce diagramme pour afficher les effets, vous devez en évaluer la signification statistique à l'aide d'un tableau d'analyse de la variance.
Ce diagramme affiche les moyennes des données. Si l'utilisation des moyennes de données peut donner une idée générale des effets les plus évidents, il est généralement recommandé d'utiliser les moyennes ajustées dans Diagrammes factoriels pour obtenir des résultats plus précis.