Test de Wilks
La statistique du test, le lambda de Wilks, est calculée comme suit :
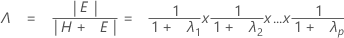
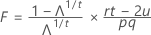
avec pq et (rt – 2u) DL.
Notation
| Terme | Description |
|---|---|
| H | matrice d'hypothèses |
| E | matrice d'erreurs |
| p | nombre de réponses |
| q | DL de l'hypothèse |
| v | DL pour E |
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| s | 0,25 (pq – 2) |
| t | = racine carrée ([p2 q2 - 4] / p2 + q2 - 5, si p2 + q2 - 5 > 0 |
| t | 1 |
Soient λ1≥λ2≥λ3≥ . . . ≥λp les valeurs propres de (E** - 1) * H. Les trois premières statistiques de test peuvent être exprimées en fonction de H et de E, ou de ces valeurs propres.
La matrice H est une matrice p x p qui contient la somme des carrés "à l'intérieur" sur la diagonale pour chaque variable p. La matrice H est calculée comme suit :

La matrice H est une matrice p x p qui contient la somme des carrés "à l'intérieur" sur la diagonale pour chaque variable p. . La matrice E est calculée comme suit :
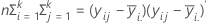
Dans les trois premiers tests, la statistique F est exacte si s = 1 ou 2 ; sinon, elle est approximée. Minitab vous indique lorsque le test est approximatif.
Test de Lawley-Hotelling
La statistique du test, la trace de Lawley-Hotelling, est calculée comme suit :

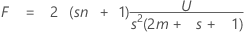
avec s (2m + s + 1) et 2 (sn + 1) DL.
Notation
| Terme | Description |
|---|---|
| H | matrice d'hypothèses |
| E | matrice d'erreurs |
| p | nombre de réponses |
| q | DL de l'hypothèse |
| v | DL pour E |
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| u | 0,25 (pq – 2) |
| t | = racine carrée ([p2 q2 - 4] / p2 + q2 - 5, si p2 + q2 - 5 > 0 |
| t | 1 |
Soit λ1 ≥ λ2 ≥ λ3 ≥ ... ≥ λp les valeurs propres de (E** - 1) * H. Les trois premières statistiques de test peuvent être exprimées en fonction de H et de E, ou de ces valeurs propres.
La matrice H est une matrice p x p dont la diagonale contient la somme des carrés "entre" pour chacune des variables p. La matrice H est calculée comme suit :

La matrice E est une matrice p x p dont la diagonale contient la somme des carrés "à l'intérieur" pour chacune des variables p. La matrice E est calculée comme suit :
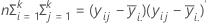
Dans les trois premiers tests, la statistique F est exacte si s = 1 ou 2 ; sinon, elle est approximée. Minitab vous indique lorsque le test est approximatif.
Test de Pillai
La statistique du test, la trace de Pillai, est calculée comme suit :


Notation
| Terme | Description |
|---|---|
| H | matrice d'hypothèses |
| E | matrice d'erreurs |
| p | nombre de réponses |
| q | DL de l'hypothèse |
| v | DL pour E |
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| u | 0,25 (pq – 2) |
| t | = racine carrée ([p2 q2 - 4] / p2 + q2 - 5, si p2 + q2 - 5 > 0 |
| t | 1 |
Soit λ1 ≥ λ2 ≥ λ3 ≥ ... ≥ λp les valeurs propres de (E** - 1) * H. Les trois premières statistiques de test peuvent être exprimées en fonction de H et de E, ou de ces valeurs propres.
La matrice H est une matrice p x p dont la diagonale contient la somme des carrés "entre" pour chacune des variables p. La matrice H est calculée comme suit :

La matrice E est une matrice p x p dont la diagonale contient la somme des carrés "à l'intérieur" pour chacune des variables p. La matrice E est calculée comme suit :
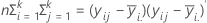
Dans les trois premiers tests, la statistique F est exacte si s = 1 ou 2 ; sinon, elle est approximée. Minitab vous indique lorsque le test est approximatif.
Test de la plus grande racine de Roy
Valeur propre la plus élevée, λ1. Pour terminer le test, vous devez utiliser des graphiques spéciaux, nommés graphiques de Heck, ainsi que les paramètres s, m et n, afin de connaître le seuil de signification.
Reportez-vous à Heck1 pour plus d'informations sur ces graphiques.
Notation
| Terme | Description |
|---|---|
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
Soit λ1 ≥ λ2 ≥ λ3 ≥ ... ≥λp les valeurs propres de (E** - 1) * H. Les trois premières statistiques de test peuvent être exprimées en fonction de H et de E, ou de ces valeurs propres.
- D.L. Heck (1960), "Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root", The Annals of Statistics, 625–642.
