Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
Coefficient (Coeff)
Pour la matrice, voici la formule permettant de calculer le vecteur des coefficients dans le modèle :

Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| Y | vecteur de réponse |
Erreur type du coefficient (Coef ErT)
Les erreurs types des coefficients pour la régression multiple sont les racines carrées des éléments de la diagonale de cette matrice :
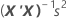
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| X' | transposition de la matrice de plan |
| s2 | carré moyen de l'erreur |
Valeur de t

Notation
| Terme | Description |
|---|---|
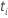 | statistique de test pour l' coefficient coefficient |
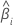 |  coefficient estimé coefficient estimé |
 | erreur type de l'  coefficient estimé coefficient estimé |
Valeur de p - Tableau des coefficients
La valeur de p bilatérale pour l'hypothèse nulle selon laquelle un coefficient de régression est égal à 0 est calculée comme suit :
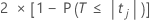
Les degrés de liberté pour l'erreur sont calculés comme suit :
n – p – 1
Notation
| Terme | Description |
|---|---|
 | fonction de répartition de la loi t, où le nombre de degrés de liberté est égal au nombre de degrés de liberté pour l'erreur |
| tj | statistique t du je coefficient |
| n | nombre d'observations dans l'ensemble de données |
| p | somme des degrés de liberté pour les termes, constant non incluse |
