Sur ce thème
- Etape 1 : Tester l'égalité des moyennes de toutes les réponses
- Etape 2 : Déterminer les moyennes de réponse dont les différences sont les plus importantes pour chaque facteur
- Etape 3 : Evaluer les différences entre les moyennes de groupes
- Etape 4 : Evaluer les résultats univariés pour examiner les réponses individuelles
- Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Etape 1 : Tester l'égalité des moyennes de toutes les réponses
- Valeur de p ≤ α : les différences entre les moyennes sont statistiquement significatives.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez en conclure que les différences entre les moyennes sont statistiquement significatives.
- Valeur de p > α : les différences entre certaines moyennes ne sont pas statistiquement significatives.
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure que les différences entre les moyennes sont statistiquement significatives. Il est sans doute nécessaire de réajuster le modèle sans le terme.
- Si un effet principal est significatif, les moyennes des niveaux du facteur sont significativement différentes les unes des autres pour toutes les réponses de votre modèle.
- Si un terme d'interaction est significatif, les effets de chaque facteur sont différents à chaque niveau des autres facteurs pour toutes les réponses de votre modèle. Pour cette raison, n'analysez pas les effets individuels de termes impliqués dans des interactions d'ordre supérieur qui sont significatives.
Tests de MANOVA de Méthode
| Statistique du test | DL | ||||
|---|---|---|---|---|---|
| Critère | F | Nombre | Dénominateur | P | |
| De Wilk | 0,63099 | 16,082 | 2 | 55 | 0,000 |
| Lawley-Hotelling | 0,58482 | 16,082 | 2 | 55 | 0,000 |
| De Pillai | 0,36901 | 16,082 | 2 | 55 | 0,000 |
| De Roy | 0,58482 | ||||
Tests de MANOVA de Usine
| Statistique du test | DL | ||||
|---|---|---|---|---|---|
| Critère | F | Nombre | Dénominateur | P | |
| De Wilk | 0,89178 | 1,621 | 4 | 110 | 0,174 |
| Lawley-Hotelling | 0,11972 | 1,616 | 4 | 108 | 0,175 |
| De Pillai | 0,10967 | 1,625 | 4 | 112 | 0,173 |
| De Roy | 0,10400 | ||||
Tests de MANOVA de Méthode*Usine
| Statistique du test | DL | ||||
|---|---|---|---|---|---|
| Critère | F | Nombre | Dénominateur | P | |
| De Wilk | 0,85826 | 2,184 | 4 | 110 | 0,075 |
| Lawley-Hotelling | 0,16439 | 2,219 | 4 | 108 | 0,072 |
| De Pillai | 0,14239 | 2,146 | 4 | 112 | 0,080 |
| De Roy | 0,15966 | ||||
Résultats principaux : P
Les valeurs de p pour la méthode de production sont statistiquement significatives au seuil de signification de 0,10. Les valeurs de p pour l'usine de fabrication ne sont significatives pour aucun des tests au seuil de signification de 0,10. Les valeurs de p pour l'interaction entre l'usine et la méthode sont statistiquement significatives au seuil de signification de 0,10. Etant donné que l'interaction est statistiquement significative, l'effet de la méthode dépend de l'usine.
Etape 2 : Déterminer les moyennes de réponse dont les différences sont les plus importantes pour chaque facteur
Utilisez l'analyse des valeurs et vecteurs propres pour déterminer comment les moyennes de réponse diffèrent entre les niveaux des différents termes du modèle. Vous devez vous concentrer sur les vecteurs propres qui correspondent à des valeurs propres élevées. Pour afficher l'analyse des valeurs et vecteurs propres, accédez à et sélectionnez Analyse des valeurs et vecteurs propres sous Affichage des résultats.
Analyse des valeurs et vecteurs propres de Méthode
| Valeur propre | 0,5848 | 0,00000 |
|---|---|---|
| Proportion | 1,0000 | 0,00000 |
| Cumulée | 1,0000 | 1,00000 |
| Vecteur propre | 1 | 2 |
|---|---|---|
| Eval commodité | 0,144062 | -0,07870 |
| Eval qualité | -0,003968 | 0,13976 |
Résultat principal : valeur propre, vecteur propre
Dans ces résultats, la première valeur propre pour la méthode (0,5848) est supérieure à la deuxième (0,00). Ainsi, vous devez accorder plus d'importance au premier vecteur. Le premier vecteur propre pour la méthode est 0,144062, -0,003968. La valeur absolue la plus élevée dans ce vecteur est celle qui correspond à l'évaluation de la commodité. Cela suggère que les moyennes de commodité présentent la différence la plus importante entre les niveaux de facteur pour la méthode. Ces informations sont utiles pour interpréter le tableau des moyennes.
Etape 3 : Evaluer les différences entre les moyennes de groupes
Utilisez le tableau des moyennes pour voir les différences qui sont statistiquement significatives entre les niveaux de facteurs dans vos données. La moyenne de chaque groupe fournit une estimation de la moyenne de chaque population. Recherchez les différences entre les moyennes des groupes pour les termes qui sont statistiquement significatifs.
Pour les effets principaux, le tableau affiche les groupes propres à chaque facteur, ainsi que leurs moyennes. Pour les effets d'interaction, le tableau affiche toutes les combinaisons de groupes possibles. Si un terme d'interaction est statistiquement significatif, vous ne pouvez pas interpréter les effets principaux sans tenir compte des effets d'interaction.
Pour afficher les moyennes, accédez à , sélectionnez Analyse de la variance univariée et entrez les termes dans la zone Afficher les moyennes issues des moindres carrés correspondant aux termes.
Moyennes issues des moindres carrés pour les réponses
| Eval commodité | Eval qualité | |||
|---|---|---|---|---|
| Moyenne | ErT moyenne | Moyenne | ErT moyenne | |
| Méthode | ||||
| Méthode 1 | 4,819 | 0,165 | 5,242 | 0,193 |
| Méthode 2 | 6,212 | 0,179 | 6,026 | 0,211 |
| Usine | ||||
| Usine A | 5,708 | 0,192 | 5,833 | 0,226 |
| Usine B | 5,493 | 0,232 | 5,914 | 0,273 |
| Usine C | 5,345 | 0,206 | 5,155 | 0,242 |
| Méthode*Usine | ||||
| Méthode 1 Usine A | 4,667 | 0,272 | 5,417 | 0,319 |
| Méthode 1 Usine B | 4,700 | 0,298 | 5,400 | 0,350 |
| Méthode 1 Usine C | 5,091 | 0,284 | 4,909 | 0,334 |
| Méthode 2 Usine A | 6,750 | 0,272 | 6,250 | 0,319 |
| Méthode 2 Usine B | 6,286 | 0,356 | 6,429 | 0,418 |
| Méthode 2 Usine C | 5,600 | 0,298 | 5,400 | 0,350 |
Résultat principal : moyenne
Dans ces résultats, le tableau des moyennes indique dans quelle mesure les évaluations de qualité et de commodité moyennes varient en fonction de la méthode, de l'usine et de l'interaction Méthode*Usine. La méthode et le terme d'interaction sont statistiquement significatifs au seuil de 0,10. Le tableau indique que la méthode 1 et la méthode 2 sont associées à des évaluations de commodité moyennes de 4,819 et 6,212 respectivement. La différence entre ces moyennes est plus importante que la différence entre les moyennes correspondantes pour l'évaluation de la qualité. Cela confirme l'interprétation de l'analyse des valeurs et vecteurs propres.
Toutefois, étant donné que le terme d'interaction Méthode*Usine est lui aussi statistiquement significatif, vous ne pouvez pas interpréter les effets principaux sans tenir compte des effets d'interaction. Par exemple, le tableau du terme d'interaction indique qu'avec la méthode 1, l'usine C est associée à l'évaluation de commodité la plus élevée et à l'évaluation de qualité la plus faible. En revanche, avec la méthode 2, l'usine A est associée à l'évaluation de commodité la plus élevée et à une évaluation de qualité qui est presque égale à la plus élevée.
Etape 4 : Evaluer les résultats univariés pour examiner les réponses individuelles
Lorsque vous effectuez une MANOVA générale, vous pouvez choisir de calculer les statistiques univariées pour examiner les réponses individuelles. Les résultats univariés permettent parfois de comprendre plus simplement les relations au sein de vos données. Toutefois, les résutlats univariés peuvent être différents des résultats multivariés.
Pour afficher les résultats univariés, accédez à et sélectionnez Analyse de la variance univariée sous Affichage des résultats.
- Valeur de p ≤ α : l'association est statistiquement significative.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme.
- Valeur de p > α : l'association n'est pas statistiquement significative.
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme. Il est sans doute nécessaire de réajuster le modèle sans le terme.
- Si un facteur de catégorie est significatif, vous pouvez en conclure que les moyennes des niveaux ne sont pas toutes égales.
- Si un terme d'interaction est significatif, la relation entre l'un des facteurs et la réponse dépend des autres facteurs du terme. Dans ce cas, vous ne devez pas interpréter les effets principaux sans prendre en compte l'effet d'interaction.
- Si une covariable est statistiquement significative, vous pouvez en conclure qu'une variation de la valeur de la covariable entraîne une variation de la valeur de réponse moyenne.
- Si un terme polynomial est significatif, vous pouvez en conclure que les données contiennent une courbure.
Analyse de la variance pour Eval commodité, avec utilisation de la somme des carrés ajustée pour les tests
| Source | DL | SomCar séq | SomCar ajust | CM ajust | F | P |
|---|---|---|---|---|---|---|
| Méthode | 1 | 31,264 | 29,074 | 29,0738 | 32,72 | 0,000 |
| Usine | 2 | 1,366 | 1,499 | 0,7495 | 0,84 | 0,436 |
| Méthode*Usine | 2 | 7,099 | 7,099 | 3,5494 | 3,99 | 0,024 |
| Erreur | 56 | 49,754 | 49,754 | 0,8885 | ||
| Total | 61 | 89,484 |
Analyse de la variance pour Eval qualité, avec utilisation de la somme des carrés ajustée pour les tests
| Source | DL | SomCar séq | SomCar ajust | CM ajust | F | P |
|---|---|---|---|---|---|---|
| Méthode | 1 | 8,8587 | 9,2196 | 9,2196 | 7,53 | 0,008 |
| Usine | 2 | 6,7632 | 7,0572 | 3,5286 | 2,88 | 0,064 |
| Méthode*Usine | 2 | 0,7074 | 0,7074 | 0,3537 | 0,29 | 0,750 |
| Erreur | 56 | 68,5900 | 68,5900 | 1,2248 | ||
| Total | 61 | 84,9194 |
Résultats principaux : P
Dans ces résultats, les valeurs de p pour l'effet principal de la méthode et pour l'effet d'interaction Méthode*Usine sont statistiquement significatifs au seuil de 0,10 du modèle pour l'évaluation de la commodité. Les effets principaux de la méthode et de l'usine sont statistiquement significatifs dans le modèle pour l'évaluation de la qualité. Vous pouvez en conclure que la variation de ces variables entraîne une variation des variables de réponses.
Etape 5 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
Lorsque vous utilisez la fonction MANOVA générale, Minitab affiche des graphiques des valeurs résiduelles pour toutes les variables de réponse contenues dans votre modèle. Vous devez déterminer si les graphiques des valeurs résiduelles de toutes les variables de réponse indiquent que le modèle vérifie les hypothèses.
Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Graphiques des valeurs résiduelles pour la fonction MANOVA générale et cliquez sur le nom du graphique des valeurs résiduelles dans la liste située en haut de la page.
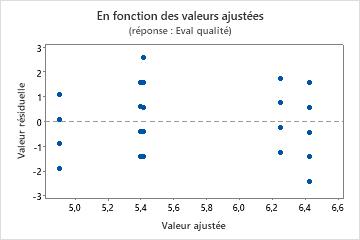
Graphique des valeurs résiduelles en fonction des valeurs ajustées
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |
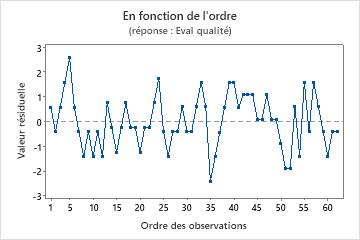
Graphique des valeurs résiduelles en fonction de l'ordre
Tendance
Equipe
Cycle
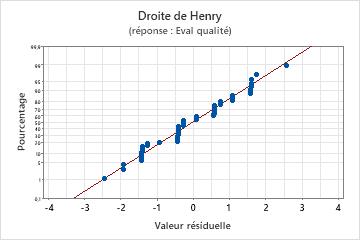
Droite de Henry des valeurs résiduelles
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
| Schéma | Ce que le schéma indique |
|---|---|
| Une ligne qui n'est pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Une modification de la pente | Une variable non identifiée |