Sur ce thème
Modèle ANOVA totalement emboîtée
Le modèle ANOVA emboîté avec un plan équilibré à deux facteurs aléatoires (A et B) est défini comme suit :
yijk = μ .. + α i+ β j(i) +εijk
où α i, β j(i) et ε ijk sont des variables aléatoires indépendantes suivant la loi normale avec des prévisions de 0 et des variances respectives σ2α, σ2β et σ2.
Les paramètres sont estimés de la manière suivante :
μ .. = y̅...
α i = yi..− y̅...
β j(i) = yij.− y̅i..
où y̅... = la moyenne de toutes les observations, yi.. = la moyenne des observations à l'ie niveau du facteur A, yij. = la moyenne des observations pour le je niveau du facteur B à l'ie niveau du facteur A. Le paramètre β j(i) est l'effet spécifique de B à l'ie niveau de A.
- J. Neter, W. Wasserman et M.H. Kutner (1985) Applied Linear Statistical Models. 2e édition. Irwin, Inc.
Somme des carrés séquentielle
Somme des carrés des distances. SC totale représente la variation totale des données. SC (A) et SC (B) représentent la variation de la moyenne de niveau de facteur estimée autour de la moyenne globale. Ces valeurs sont également appelées somme des carrés pour le facteur A ou B. SC Erreur est la variation des observations par rapport à leurs valeurs ajustées. Les calculs sont les suivants :
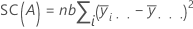
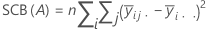
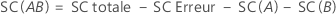


Minitab fournit la somme des carrés séquentielle, qui dépend de l'ordre dans lequel les facteurs sont entrés dans le modèle. Il s'agit de la part de la somme des carrés de la régression expliquée par un facteur unique, en fonction de tous les autres facteurs déjà entrés.
Notation
| Terme | Description |
|---|---|
| a | nombre de niveaux dans le facteur A |
| b | nombre de niveaux dans le facteur B |
| n | nombre total d'essais |
| yi.. | moyenne de l'ie niveau du facteur A |
| y... | moyenne globale de toutes les observations |
| y.j. | moyenne du je niveau du facteur B |
| yij. | moyenne des observations à l'ie niveau du facteur A et au je niveau du facteur B |
Degrés de liberté (DL)
Pour un modèle ANOVA totalement emboîté à deux facteurs (A et B), les degrés de liberté sont calculés comme suit :




où a est le nombre de niveaux du facteur A, b est le nombre de niveaux du facteur B et n est le nombre d'essais.
Carré moyen (CM)
Formules



F
Les formules suivantes sont celles utilisées pour le calcul des statistiques F pour un modèle à facteurs aléatoires.
Formules


Valeur de p - Tableau d'analyse de la variance
La valeur de p est une probabilité calculée à partir d'une loi F avec les degrés de liberté (DL) suivants :
- DL en numérateur
- somme des degrés de liberté pour le ou les termes du test
- DL en dénominateur
- degrés de liberté pour l'erreur
Formule
1 − P(F ≤ fj)
Notation
| Terme | Description |
|---|---|
| P(F ≤ f) | fonction de répartition de la loi F |
| f | statistique f pour le test |
Composantes de la variance
Calculées pour les facteurs aléatoires. Le modèle emboîté à deux facteurs aléatoires est le suivant :
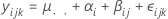
où αi, βj(i) et εijk sont des variables aléatoires indépendantes suivant la loi normale. Les variables sont distribuées normalement avec une moyenne de zéro et des variances données par V(αi) = σ2α, V(βj) = σ2β et V(εijk) = σ2. Nous supposons que toutes les valeurs de bj(i) ont la même variance. σ2β, σ2α, σ2β, σ2αβ, σ2 sont appelées composantes de la variance.
Espérance mathématique des carrés moyens
Pour un modèle à deux facteurs aléatoires A et B, l'espérance mathématique des carrés moyens est calculée comme suit :
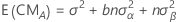

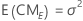
Statistique F pour les modèles avec facteurs aléatoires
Méthode de calcul des statistiques F dans les résultats de l'ANOVA
Chaque statistique F est un rapport de carrés moyens. Le numérateur est le carré moyen associé au terme. Le dénominateur est également un carré moyen, choisi de façon à ce que la différence entre le numérateur et le dénominateur corresponde à l'effet qui vous intéresse. L'effet d'un terme aléatoire est représenté par la composante de variance de ce terme. L'effet d'un terme fixe est représenté par la somme des carrés des composantes du modèle associées à ce terme, divisée par ses degrés de liberté. Par conséquent, une statistique F élevée indique que l'effet est significatif.
Lorsque tous les termes du modèle sont fixes, le dénominateur de chaque statistique F est le carré moyen de l'erreur. En revanche, pour les modèles comprenant des termes aléatoires, le carré moyen de l'erreur n'est pas toujours le dénominateur approprié. Vous pouvez utiliser l'espérance mathématique des carrés moyens pour déterminer la valeur appropriée pour le dénominateur.
Exemple
| Source | Espérance mathématique des carrés moyens pour chaque terme |
|---|---|
| (1) Filtre | (4) + 2,0000(3) + Q[1] |
| (2) Tech | (4) + 2,0000(3) + 4,0000(2) |
| (3) Filtre*Tech | (4) + 2,0000(3) |
| (4) Erreur | (4) |
Les nombres entre parenthèses désignent l'effet aléatoire du terme qui leur est associé dans la colonne Source. (2) représente l'effet aléatoire de Tech, (3) représente l'effet aléatoire de l'interaction Filtre*Tech et (4) représente l'effet aléatoire de l'erreur. L'espérance mathématique des carrés moyens pour Erreur est l'effet du terme d'erreur. En outre, l'espérance mathématique des carrés moyens pour Filtre*Tech est l'effet du terme d'erreur plus deux fois l'effet de l'interaction Filtre*Tech.
Pour calculer la statistique F pour Filtre*Tech, le carré moyen de Filtre*Tech est divisé par celui de l'erreur ; ainsi la valeur attendue du numérateur (espérance mathématique des carrés moyens pour Filtre*Tech = (4) + 2,0000(3)) ne diffère de la valeur attendue du dénominateur (espérance mathématique des carrés moyens pour Erreur = (4)) que par l'effet de l'interaction (2,0000(3)). Par conséquent, une statistique F élevée indique que l'interaction Filtre*Tech est significative.
Les nombres avec Q[ ] désignent l'effet fixe du terme qui leur est associé dans la colonne Source. Par exemple, Q[1] représente l'effet fixe de Filtre. L'espérance mathématique des carrés moyens pour Filtre correspond à l'effet du terme d'erreur plus deux fois l'effet de l'interaction Filtre*Tech, plus l'effet de Filtre multiplié par une valeur constante. Q[1] est égal à (b*n*somme((coefficients des niveaux de Filtre)**2)) divisé par (a - 1), où a et b représentent respectivement le nombre de niveaux de Filtre et Tech, et n représente le nombre de répétitions.
Pour calculer la statistique F pour Filtre, le carré moyen de Filtre est divisé par celui de Filtre*Tech ; ainsi la valeur attendue du numérateur (espérance mathématique des carrés moyens pour Filtre = (4) + 2,0000(3) + Q[1]) ne diffère de la valeur attendue du dénominateur (espérance mathématique des carrés moyens pour Filtre*Tech = (4) + 2,0000(3)) que par l'effet de Filtre (Q[1]). Par conséquent, une statistique F élevée indique que l'effet de Filtre est significatif.
Pourquoi le résultat de mon analyse ANOVA comporte-t-elle un "x" à côté d'une valeur de p dans le tableau ANOVA, ainsi que la mention "n'est pas un test F exact" ?
Pour un terme donné, le test F est dit exact lorsque la différence entre le numérateur (carré moyen attendu pour le terme) et le dénominateur est uniquement constituée par la composante de variance ou le facteur fixe qui vous intéresse.
Toutefois, il peut arriver que le carré moyen à utiliser comme dénominateur ne puisse pas être calculé. Dans ce cas, Minitab utilise un carré moyen permettant d'obtenir un test F approximatif et affiche un "x" à côté de la valeur de p pour indiquer que le test F n'est pas exact.
| Source | Espérance mathématique des carrés moyens pour chaque terme |
|---|---|
| (1) Complément | (4) + 1,7500(3) + Q[1] |
| (2) Laque | (4) + 1,7143(3) + 5,1429(2) |
| (3) Complément*Laque | (4) + 1,7500(3) |
| (4) Erreur | (4) |
La statistique F pour Complément est le carré moyen de celui-ci divisé par le carré moyen de l'interaction Complément*Laque. Si l'effet pour Complément est très faible, la valeur attendue du numérateur est égale à la valeur attendue du dénominateur. Ceci est un exemple d'un test F exact.
Remarquez en revanche que pour un effet Laque très faible, il n'y a aucun carré moyen qui fasse que la valeur attendue du numérateur soit égale à la valeur attendue du dénominateur. Par conséquent, Minitab utilise un test F approximatif. Dans cet exemple, le carré moyen de Laque est divisé par celui de l'interaction Complément*Laque. Cette opération donne une valeur attendue du numérateur approximativement égale à celle du dénominateur si l'effet Laque est très faible.
A propos du message "Le dénominateur du test F est nul ou non défini"
- L'erreur ne dispose d'aucun degré de liberté.
-
Les valeurs du CM ajusté sont très faibles, d'où un manque de précision empêchant d'afficher les valeurs F et de p. Pour contourner ce problème, vous pouvez multiplier la colonne de réponse par 10. Ensuite, appliquez le même modèle de régression, mais en utilissant cette nouvelle colonne pour la réponse.
Remarque
Le fait de multiplier les valeurs de réponse par 10 n'aura pas d'incidence sur les valeurs de F et de p affichées dans les résultats par Minitab. En revanche, la position des décimales dans le reste des résultats sera modifiée, en particulier dans les colonnes SomCar ajust, CM ajust et Ajus, ainsi que dans celles des sommes des carrés séquentielles, de l'erreur type des valeurs ajustées et des valeurs résiduelles.
Méthode de calcul des statistiques F dans les résultats de l'ANOVA
Chaque statistique F est un rapport de carrés moyens. Le numérateur est le carré moyen associé au terme. Le dénominateur est également un carré moyen, choisi de façon à ce que la différence entre le numérateur et le dénominateur corresponde à l'effet qui vous intéresse. L'effet d'un terme aléatoire est représenté par la composante de variance de ce terme. L'effet d'un terme fixe est représenté par la somme des carrés des composantes du modèle associées à ce terme, divisée par ses degrés de liberté. Par conséquent, une statistique F élevée indique que l'effet est significatif.
Lorsque tous les termes du modèle sont fixes, le dénominateur de chaque statistique F est le carré moyen de l'erreur. En revanche, pour les modèles comprenant des termes aléatoires, le carré moyen de l'erreur n'est pas toujours le dénominateur approprié. Vous pouvez utiliser l'espérance mathématique des carrés moyens pour déterminer la valeur appropriée pour le dénominateur.
Exemple
| Source | Espérance mathématique des carrés moyens pour chaque terme |
|---|---|
| (1) Filtre | (4) + 2,0000(3) + Q[1] |
| (2) Tech | (4) + 2,0000(3) + 4,0000(2) |
| (3) Filtre*Tech | (4) + 2,0000(3) |
| (4) Erreur | (4) |
Les nombres entre parenthèses désignent l'effet aléatoire du terme qui leur est associé dans la colonne Source. (2) représente l'effet aléatoire de Tech, (3) représente l'effet aléatoire de l'interaction Filtre*Tech et (4) représente l'effet aléatoire de l'erreur. L'espérance mathématique des carrés moyens pour Erreur est l'effet du terme d'erreur. En outre, l'espérance mathématique des carrés moyens pour Filtre*Tech est l'effet du terme d'erreur plus deux fois l'effet de l'interaction Filtre*Tech.
Pour calculer la statistique F pour Filtre*Tech, le carré moyen de Filtre*Tech est divisé par celui de l'erreur ; ainsi la valeur attendue du numérateur (espérance mathématique des carrés moyens pour Filtre*Tech = (4) + 2,0000(3)) ne diffère de la valeur attendue du dénominateur (espérance mathématique des carrés moyens pour Erreur = (4)) que par l'effet de l'interaction (2,0000(3)). Par conséquent, une statistique F élevée indique que l'interaction Filtre*Tech est significative.
Les nombres avec Q[ ] désignent l'effet fixe du terme qui leur est associé dans la colonne Source. Par exemple, Q[1] représente l'effet fixe de Filtre. L'espérance mathématique des carrés moyens pour Filtre correspond à l'effet du terme d'erreur plus deux fois l'effet de l'interaction Filtre*Tech, plus l'effet de Filtre multiplié par une valeur constante. Q[1] est égal à (b*n*somme((coefficients des niveaux de Filtre)**2)) divisé par (a - 1), où a et b représentent respectivement le nombre de niveaux de Filtre et Tech, et n représente le nombre de répétitions.
Pour calculer la statistique F pour Filtre, le carré moyen de Filtre est divisé par celui de Filtre*Tech ; ainsi la valeur attendue du numérateur (espérance mathématique des carrés moyens pour Filtre = (4) + 2,0000(3) + Q[1]) ne diffère de la valeur attendue du dénominateur (espérance mathématique des carrés moyens pour Filtre*Tech = (4) + 2,0000(3)) que par l'effet de Filtre (Q[1]). Par conséquent, une statistique F élevée indique que l'effet de Filtre est significatif.
Pourquoi le résultat de mon analyse ANOVA comporte-t-elle un "x" à côté d'une valeur de p dans le tableau ANOVA, ainsi que la mention "n'est pas un test F exact" ?
Pour un terme donné, le test F est dit exact lorsque la différence entre le numérateur (carré moyen attendu pour le terme) et le dénominateur est uniquement constituée par la composante de variance ou le facteur fixe qui vous intéresse.
Toutefois, il peut arriver que le carré moyen à utiliser comme dénominateur ne puisse pas être calculé. Dans ce cas, Minitab utilise un carré moyen permettant d'obtenir un test F approximatif et affiche un "x" à côté de la valeur de p pour indiquer que le test F n'est pas exact.
| Source | Espérance mathématique des carrés moyens pour chaque terme |
|---|---|
| (1) Complément | (4) + 1,7500(3) + Q[1] |
| (2) Laque | (4) + 1,7143(3) + 5,1429(2) |
| (3) Complément*Laque | (4) + 1,7500(3) |
| (4) Erreur | (4) |
La statistique F pour Complément est le carré moyen de celui-ci divisé par le carré moyen de l'interaction Complément*Laque. Si l'effet pour Complément est très faible, la valeur attendue du numérateur est égale à la valeur attendue du dénominateur. Ceci est un exemple d'un test F exact.
Remarquez en revanche que pour un effet Laque très faible, il n'y a aucun carré moyen qui fasse que la valeur attendue du numérateur soit égale à la valeur attendue du dénominateur. Par conséquent, Minitab utilise un test F approximatif. Dans cet exemple, le carré moyen de Laque est divisé par celui de l'interaction Complément*Laque. Cette opération donne une valeur attendue du numérateur approximativement égale à celle du dénominateur si l'effet Laque est très faible.
A propos du message "Le dénominateur du test F est nul ou non défini"
- L'erreur ne dispose d'aucun degré de liberté.
-
Les valeurs du CM ajusté sont très faibles, d'où un manque de précision empêchant d'afficher les valeurs F et de p. Pour contourner ce problème, vous pouvez multiplier la colonne de réponse par 10. Ensuite, appliquez le même modèle de régression, mais en utilissant cette nouvelle colonne pour la réponse.
Remarque
Le fait de multiplier les valeurs de réponse par 10 n'aura pas d'incidence sur les valeurs de F et de p affichées dans les résultats par Minitab. En revanche, la position des décimales dans le reste des résultats sera modifiée, en particulier dans les colonnes SomCar ajust, CM ajust et Ajus, ainsi que dans celles des sommes des carrés séquentielles, de l'erreur type des valeurs ajustées et des valeurs résiduelles.
