Sur ce thème
Modèle MLG
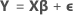
Notation
| Terme | Description |
|---|---|
| Y | vecteur de réponses |
| X | matrice du plan |
| β | vecteur de paramètres |
| ε | vecteur de variables aléatoires indépendantes suivant la loi normale |
Matrice du plan
La fonction Modèle linéaire général utilise une approche par régression pour ajuster le modèle que vous spécifiez. Minitab crée d'abord une matrice du plan d'expériences à partir des facteurs, des covariables et du modèle que vous spécifiez. Les colonnes de cette matrice sont les prédicteurs pour la régression.
La matrice du plan contient n lignes, où n est le nombre d'observations, et plusieurs blocs de colonnes, correspondant aux termes du modèle. Le premier bloc correspond à la constante et ne contient qu'une colonne constituée uniquement de 1. Le bloc pour une covariable contient lui aussi seulement une colonne, la colonne de la covariable elle-même. Le bloc de colonnes correspondant à un facteur contient r colonnes, où r est le nombre de degrés de liberté pour le facteur, et elles sont codées tel qu'indiqué dans l'exemple ci-dessous.
Supposons que A soit un facteur avec 4 niveaux. Il a alors 3 degrés de liberté et son bloc contient 3 colonnes que l'on appellera A1, A2, A3.
| Niveau de A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | –1 | –1 | –1 |
Supposons que le facteur B a 3 niveaux emboîtés dans chaque niveau de A. Son bloc contient alors (3 - 1) x 4 = 8 colonnes que l'on appellera B11, B12, B21, B22, B31, B32, B41, B42, codées de la façon suivante :
| Niveau de A | Niveau de B | B11 | B12 | B21 | B22 | B31 | B32 | B41 | B42 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | –1 | –1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | –1 |
Pour calculer les colonnes correspondant à un terme d'interaction, il suffit de multiplier toutes les colonnes correspondantes pour les facteurs et/ou les covariables dans l'interaction. Par exemple, supposons que A comporte 6 niveaux, C 3 niveaux, D 4 niveaux et que Z et W soient des covariables. Le terme A*C*D*Z*W*W aura 5 x 2 x 3 x 1 x 1 x 1 = 30 colonnes. Pour les obtenir, multipliez chaque colonne de A par les colonnes de C, puis par les colonnes de D, puis une fois par la covariable Z et deux fois par la covariable W.
Transformation de Box-Cox
La transformation de Box-Cox sélectionne les valeurs lambda (comme indiqué ci-dessous) qui minimisent la somme des carrés des valeurs résiduelles. La transformation obtenue est Y λ lorsque λ ≠ 0, et ln(Y) lorsque λ = 0. Lorsque λ < 0, Minitab multiplie également la réponse transformée par −1 pour conserver l'ordre de la réponse non transformée.
Minitab recherche une valeur optimale entre −2 et 2. Les valeurs en dehors de cet intervalle sont susceptibles de ne pas fournir un meilleur ajustement.
Voici quelques transformations courantes dans lesquelles Y′ représente la transformation des données Y :
| Valeur lambda (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 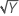 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Régression pondérée
La régression par les moindres carrés pondérée est une méthode permettant de traiter les observations qui présentent des variances non constantes. Si les variances ne sont pas constantes, attribuez :
- des pondérations relativement faibles aux observations ayant des variances importantes
- des pondérations relativement importantes aux observations ayant des variances faibles
Les pondérations sont généralement choisies comme l'inverse de la variance de l'erreur pure dans le réponse.
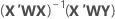
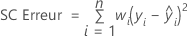
Notation
| Terme | Description |
|---|---|
| X | matrice du plan |
| X' | transposition de la matrice de plan |
| W | matrice n x n, avec les pondérations sur la diagonale |
| Y | vecteur des valeurs de réponse |
| n | nombre d'observations |
| wi | pondération pour l'ie observation |
| yi | valeur de réponse pour l'ie observation |
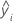 | valeur ajustée pour l'ie observation |
Procédure pour supprimer des prédicteurs fortement corrélés de l'équation de régression dans Ajuster le modèle linéaire général
- Minitab effectue une décomposition QR sur la matrice X.
Remarque
Il est plus rapide d'utiliser la décomposition QR pour calculer le R2 que la régression sur les moindres carrés.
- Minitab effectue une régression d'un prédicteur sur tous les autres prédicteurs et calcule la valeur de R2. Si 1 – R2 < 4 * 2,22e-16, le prédicteur échoue au test et est supprimé du modèle.
- Minitab répète les étapes 1 et 2 pour le reste des prédicteurs.
Exemple
- Minitab effectue une régression de X5 sur X1-X4. Si 1 – R2 est supérieur à 4 * 2,22e-16, X5 reste dans l'équation. X5 réussit le test et est conservé dans l'équation.
- Minitab effectue une régression de X4 sur X1, X2, X3 et X5. Supposons que 1 – R2 pour cette régression est supérieur à 4 * 2,22e-16, ce prédicteur est conservé dans l'équation.
- Minitab effectue une régression de X3 sur X1, X2, X4 et X5, puis calcule la valeur de R2. X3 échoue au test et est supprimé de l'équation.
- Minitab effectue une nouvelle décomposition QR sur la matrice X et effectue une régression de X2 sur le reste des prédicteurs, X1, X4 et X5. X2 réussit le test.
- Minitab effectue une régression de X1 sur X2, X4 et X5. Le prédicteur échoue au test et est supprimé de l'équation.
Minitab effectue une régression de Y sur X2, X4, X5. Les résultats contiennent un message indiquant que les prédicteurs X1 et X3 ne peuvent pas être estimés et ont été supprimés du modèle.
Remarque
Vous pouvez utiliser la sous-commande TOLERANCE avec la session de commande MLG pour forcer Minitab à conserver dans le modèle un prédicteur fortement corrélé à un autre prédicteur. Cependant, diminuer la tolérance peut s'avérer dangereux, car cela peut générer des résultats imprécis sur le plan numérique.
