Sur ce thème
Etape 1 : Déterminer si l'association entre la réponse et le terme est statistiquement significative
- Valeur de p ≤ α : l'association est statistiquement significative.
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme.
- Valeur de p > α : l'association n'est pas statistiquement significative.
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas conclure qu'il existe une association statistiquement significative entre la variable de réponse et le terme. Il est sans doute nécessaire de réajuster le modèle sans le terme.
- Si un facteur fixe est significatif, vous pouvez en conclure que les moyennes des niveaux ne sont pas toutes égales.
- Si un facteur aléatoire est significatif, vous pouvez en conclure qu'il contribue à la variation dans la réponse.
- Si un terme d'interaction est significatif, la relation entre l'un des facteurs et la réponse dépend des autres facteurs du terme. Dans ce cas, vous ne devez pas interpréter les effets principaux sans prendre en compte l'effet d'interaction.
Utilisez le tableau des moyennes pour voir les différences qui sont statistiquement significatives entre les niveaux de facteurs dans vos données. La moyenne de chaque groupe fournit une estimation de la moyenne de chaque population. Recherchez les différences entre les moyennes des groupes pour les termes qui sont statistiquement significatifs.
Pour les effets principaux, le tableau affiche les groupes propres à chaque facteur, ainsi que leurs moyennes. Pour les effets d'interaction, le tableau affiche toutes les combinaisons de groupes possibles. Si un terme d'interaction est statistiquement significatif, vous ne pouvez pas interpréter les effets principaux sans tenir compte des effets d'interaction.
Informations sur les facteurs
| Facteur | Type | Niveaux | Valeurs |
|---|---|---|---|
| Période | Fixe | 2 | 1; 2 |
| Opérateur | Aléatoire | 3 | 1; 2; 3 |
| Réglage | Fixe | 3 | 35; 44; 52 |
Analyse de la variance pour Epaisseur
| Source | DL | Somme des carrés | CM | F | P | |
|---|---|---|---|---|---|---|
| Période | 1 | 9,0 | 9,00 | 0,29 | 0,644 | |
| Opérateur | 2 | 1120,9 | 560,44 | 4,28 | 0,081 | x |
| Réglage | 2 | 15676,4 | 7838,19 | 73,18 | 0,001 | |
| Période*Opérateur | 2 | 62,0 | 31,00 | 4,34 | 0,026 | |
| Période*Réglage | 2 | 114,5 | 57,25 | 8,02 | 0,002 | |
| Opérateur*Réglage | 4 | 428,4 | 107,11 | 15,01 | 0,000 | |
| Erreur | 22 | 157,0 | 7,14 | |||
| Total | 35 | 17568,2 |
Récapitulatif du modèle
| S | R carré | R carré (ajust) |
|---|---|---|
| 2,67140 | 99,11% | 98,58% |
Termes d'erreur pour les tests
| Source | Composante de variance | Terme d'erreur | Espérance mathématique des carrés moyens pour chaque terme (avec modèle non restreint) | |
|---|---|---|---|---|
| 1 | Période | 4 | (7) + 6 (4) + Q[1; 5] | |
| 2 | Opérateur | 35,789 | * | (7) + 4 (6) + 6 (4) + 12 (2) |
| 3 | Réglage | 6 | (7) + 4 (6) + Q[3; 5] | |
| 4 | Période*Opérateur | 3,977 | 7 | (7) + 6 (4) |
| 5 | Période*Réglage | 7 | (7) + Q[5] | |
| 6 | Opérateur*Réglage | 24,994 | 7 | (7) + 4 (6) |
| 7 | Erreur | 7,136 | (7) |
Termes d'erreur pour les tests synthétisés
| Source | Erreur - DL | Erreur - CM | Synthèse du carré moyen de l'erreur | |
|---|---|---|---|---|
| 2 | Opérateur | 5,12 | 130,9747 | (4) + (6) - (7) |
Moyennes
| Période | N | Epaisseur |
|---|---|---|
| 1 | 18 | 67,7222 |
| 2 | 18 | 68,7222 |
| Réglage | N | Epaisseur |
|---|---|---|
| 35 | 12 | 40,5833 |
| 44 | 12 | 73,0833 |
| 52 | 12 | 91,0000 |
| Période*Réglage | N | Epaisseur |
|---|---|---|
| 1 35 | 6 | 40,6667 |
| 1 44 | 6 | 70,1667 |
| 1 52 | 6 | 92,3333 |
| 2 35 | 6 | 40,5000 |
| 2 44 | 6 | 76,0000 |
| 2 52 | 6 | 89,6667 |
Résultats principaux : valeur de p, tableau des moyennes
Réglage est un facteur fixe, et cet effet principal est significatif. Ce résultat indique que l'épaisseur moyenne du revêtement n'est pas la même pour tous les réglages de machine.
Période*Réglage est un effet d'interaction qui implique deux facteurs fixes. L'effet d'interaction est significatif, ce qui indique que la relation entre chaque facteur et la réponse dépend du niveau de l'autre facteur. Dans ce cas, vous ne devez pas interpréter les effets principaux sans prendre en compte l'effet d'interaction.
Dans ces résultats, le tableau des moyennes indique la variation de l'épaisseur moyenne en fonction de la période, du réglage de la machine et de chaque combinaison période/réglage de la machine. Le réglage est statistiquement significatif et les moyennes varient selon les différents réglages de la machine. Cependant, étant donné que le terme d'interaction Période*Réglage est lui aussi statistiquement significatif, vous ne pouvez pas interpréter les effets principaux sans tenir compte des effets d'interaction. Par exemple, le tableau du terme d'interaction indique qu'avec le réglage 44, la période 2 est associée à un revêtement plus épais. Par contre, avec le réglage 52, la période 1 est associée à un revêtement plus épais.
Opérateur est un facteur aléatoire et toutes les interactions qui incluent un facteur aléatoire sont considérées comme aléatoires. Si un facteur aléatoire est significatif, vous pouvez en conclure qu'il contribue à la variation dans la réponse. Le facteur Opérateur n'est pas significatif au seuil de signification de 0,05, mais les effets d'interaction qui incluent ce facteur sont eux significatifs. Ces effets d'interaction indiquent que la contribution de l'opérateur à la variation de la réponse dépend des valeurs de la période et du réglage de la machine.
Etape 2 : Déterminer l'ajustement du modèle à vos données
Pour déterminer l'ajustement du modèle aux données, étudiez les statistiques d'adéquation de l'ajustement dans le tableau Récapitulatif du modèle.
- S
-
Utilisez S pour évaluer la capacité du modèle à décrire la réponse. Utilisez S plutôt que les statistiques R2 pour comparer l'ajustement des modèles qui n'ont pas de constante.
S est mesuré en unités de la variable de réponse et représente la distance entre les valeurs de données et les valeurs ajustées. Plus S est petit, mieux le modèle décrit la réponse. Cependant, une faible valeur de S n'indique pas en soi que le modèle respecte les hypothèses du modèle. Vous devez examiner les graphiques des valeurs résiduelles pour vérifier les hypothèses.
- R carré
-
Plus la valeur R2 est élevée, plus le modèle est ajusté à vos données. R2 est toujours compris entre 0 et 100 %.
La valeur R2 augmente toujours lorsque vous ajoutez des prédicteurs à un modèle. Par exemple, le meilleur modèle à 5 prédicteurs aura toujours une valeur R2 au moins aussi élevée que celle du meilleur modèle à 4 prédicteurs. Par conséquent, R2 est surtout utile pour comparer des modèles de même taille.
- R carré (ajusté)
-
Utilisez la valeur R2 ajusté pour comparer des modèles n'ayant pas le même nombre de prédicteurs. R2 augmente toujours lorsque vous ajoutez un prédicteur au modèle, même lorsque ce prédicteur n'apporte aucune amélioration réelle au modèle. La valeur de R2 ajusté intègre le nombre de prédicteurs dans le modèle pour vous aider à choisir le modèle correct.
-
Les petits échantillons ne fournissent pas d'estimation précise de la force de la relation entre la réponse et les prédicteurs. Par exemple, pour obtenir une valeur R2 plus précise, vous devez utiliser un échantillon plus grand (en général, 40 ou plus).
-
Les statistiques d'adéquation de l'ajustement ne sont qu'un des types de mesures permettant d'évaluer l'ajustement du modèle. Même si un modèle a une valeur souhaitable, vous devez consulter les graphiques des valeurs résiduelles pour vérifier que le modèle respecte les hypothèses.
Récapitulatif du modèle
| S | R carré | R carré (ajust) |
|---|---|---|
| 2,67140 | 99,11% | 98,58% |
Résultats principaux : S, R carré, R carré (ajust)
Dans ces résultats, le modèle explique 99,11 % de la variation de l'épaisseur du revêtement. Pour ces données, la valeur de R2 indique que le modèle fournit un ajustement aux données correct. Si des modèles supplémentaires sont ajustés avec d'autres prédicteurs, utilisez les valeurs de R2 pour comparer l'ajustement des modèles aux données.
Etape 3 : Déterminer si votre modèle vérifie les hypothèses de l'analyse
Les graphiques des valeurs résiduelles permettent de déterminer si le modèle est adapté et si les hypothèses de l'analyse sont vérifiées. Si elles ne le sont pas, il se peut que le modèle ne soit pas ajusté aux données et vous devez être prudent lors de l'interprétation des résultats.
Pour plus d'informations sur la manière de traiter les schémas dans les graphiques des valeurs résiduelles, reportez-vous à la rubrique Diagrammes de valeurs résiduelles pour la fonction Ajuster le modèle linéaire général et cliquez sur le nom du graphique des valeurs résiduelles dans la liste située en haut de la page.
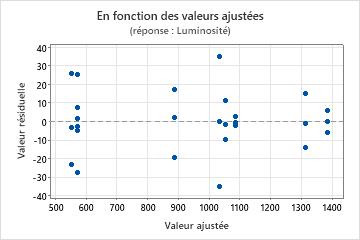
Graphique des valeurs résiduelles en fonction des valeurs ajustées
Utilisez le diagramme des valeurs résiduelles en fonction des valeurs ajustées pour vérifier l'hypothèse selon laquelle les valeurs résiduelles suivent une loi normale et ont une variance constante. Dans l'idéal, les points doivent être répartis aléatoirement des deux côtés de 0, sans schéma reconnaissable.
| Schéma | Ce que le schéma indique |
|---|---|
| Eparpillement ou répartition déséquilibrée des valeurs résiduelles en fonction des valeurs ajustées | Variance non constante |
| Curviligne | Un terme d'ordre supérieur manquant |
| Un point très éloigné de zéro | Une valeur aberrante |
| Un point éloigné des autres points dans le sens des x | Un point influent |
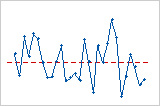
Graphique des valeurs résiduelles en fonction de l'ordre
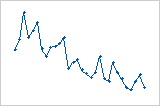
Tendance
Equipe
Cycle
Dans ce graphique des valeurs résiduelles en fonction de l'ordre, les valeurs résiduelles semblent être réparties de façon aléatoire autour de la ligne centrale. Rien ne permet de penser que les valeurs résiduelles ne sont pas indépendantes. 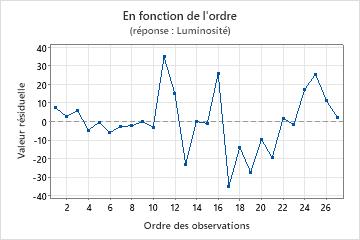
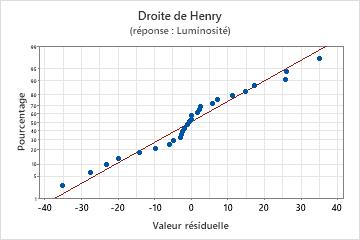
Droite de Henry
Utilisez la droite de Henry des valeurs résiduelles afin de vérifier l'hypothèse selon laquelle les valeurs résiduelles sont normalement distribuées. La droite de Henry des valeurs résiduelles doit suivre approximativement une ligne droite.
| Schéma | Ce que le schéma indique |
|---|---|
| Une ligne qui n'est pas droite | Non-normalité |
| Un point éloigné de la ligne | Une valeur aberrante |
| Une modification de la pente | Une variable non identifiée |