Sur ce thème
Méthode
L'analyse des moyennes est une procédure permettant de déterminer si les moyennes de niveaux de facteur individuels sont différentes de la moyenne générale (moyenne de toutes les observations d'un facteur). Minitab effectue les opérations suivantes pour calculer les résultats de l'ANOM pour un modèle à un facteur :
- Calcul de la moyenne à chaque niveau du facteur, y̅i. (i = 1, …, r).
- Calcul de la moyenne générale de toutes les observations, y....
- Calcul de sp, une estimation de l'écart type de l'observation.
- Etablissement de la valeur absolue hα, qui correspond à la valeur du seuil de signification choisi pour le test et est utilisée pour déterminer les lignes de décision supérieure et inférieure.
- Calcul des limites de décision supérieure et inférieure (LDS et LDI).
- Création d'un graphique des moyennes de chaque niveau de facteur avec les lignes de référence supérieure et inférieure, ainsi qu'une ligne centrale représentant la moyenne générale.
Moyenne
Formule
Moyenne des observations à chaque niveau de facteur. Minitab représente la moyenne pour chaque niveau de facteur sur le graphique.
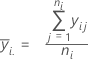
Notation
| Terme | Description |
|---|---|
| ni | nombre d'observations au niveau de facteur i |
| yij | valeur de la je observation à l'ie niveau de facteur |
Moyenne générale (ligne centrale)
Formule
Moyenne de toutes les observations pour tous les niveaux de facteurs. Minitab utilise la moyenne générale comme ligne centrale sur le graphique.
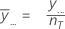
Notation
| Terme | Description |
|---|---|
| y... | somme de toutes les observations dans l'échantillon |
| nT | nombre total d'observations |
Ecart type (EcTyp)
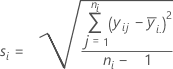
Notation
| Terme | Description |
|---|---|
| yij | observations à l'ie niveau de facteur |
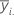 | moyenne des observations à l'ie niveau de facteur |
| ni | nombre d'observations à l'ie niveau de facteur |
Ecart type regroupé
Estimation de la variation pour l'ensemble des niveaux de facteurs. L'écart type regroupé est utilisé pour calculer les limites de décision.
Formule
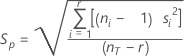
Notation
| Terme | Description |
|---|---|
| r | nombre de niveaux |
| nT | nombre total d'observations |
Limites de décision supérieure et inférieure
Les limites de décision indiquent si les moyennes des niveaux de facteurs sont différentes de la moyenne générale. Les points qui se trouvent en dehors de la limite de décision supérieure (LDS) ou inférieure (LDI) sont statistiquement différents de la moyenne générale.
Le calcul des limites de décision inférieure et supérieure varie selon le nombre de niveaux du facteur et le nombre d'observations à chaque niveau.
Facteur à deux niveaux avec le même nombre d'observations à chaque niveau
- LDS = y.. + hα sp * racine carrée(1 / nT)
- LDI = y.. - hα sp * racine carrée(1 / nT)
où hα est la valeur absolue de (t(a / 2, nT - 2)), sp est l'écart type regroupé et nT est le nombre total d'observations.
Facteur à plus de deux niveaux avec le même nombre d'observations à chaque niveau
- LDS = y.. + hα sp * racine carrée[(r - 1) / (rn1)]
- LDI = y.. - hα sp * racine carrée[(r - 1) / (rn1)]
où r est le nombre de niveaux dans le facteur et n1 est le nombre d'observations à chaque niveau.
Le nombre de degrés de liberté est égal à (n1 - 1) * r.
Pour les valeurs d'alpha en dehors de l'étendue 0,001- 0,1, les limites de décision sont calculées comme suit :
- LDS = y.. + hα sp * racine carrée[(nT - n1) / (nT * n1)]
- LDI = y.. - hα sp * racine carrée[(nT - n1) / (nT * n1)]
où hα est la valeur absolue de (t(α2, DL), et où α2 = (1 - (1 - a )** (1 / r)) / 2 et DL = nT - r.
Pour obtenir hα pour des valeurs de α comprises entre 0,001 et 0,1, reportez-vous à Nelson1.
Facteur à deux niveaux ou plus avec un nombre d'observations différent à chaque niveau
- LDSi = y.. + hα sp * racine carrée[(nT - ni) / (nT * ni)]
- LDIi = y.. - hα sp * racine carrée[(nT - ni) / (nT * ni)]
- L.S. Nelson (1983), "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
