Sur ce thème
Carte d'analyse des moyennes pour les données suivant une loi normale
La carte d'analyse des moyennes pour données normales permet de déterminer si les effets principaux et les effets d'interaction dans les données sont statistiquement significatifs. En fonction du nombre de facteurs de votre plan, la carte affiche soit un graphique des effets principaux, soit deux graphiques des effets principaux et un diagramme des effets d'interaction.
- diagramme des effets d'interaction
-
Utilisez le diagramme des effets d'interaction pour tester l'hypothèse nulle selon laquelle il n'existe aucune interaction entre les facteurs. Minitab n'affiche un diagramme des effets d'interaction que lorsque les données incluent deux facteurs.
Le diagramme des effets d'interaction indique la mesure moyenne pour chaque combinaison de niveaux de facteurs. Minitab place la ligne centrale à une valeur de zéro, qui représente l'absence d'effet d'interaction. Les limites de décision sont calculées à partir de vos données et du seuil de signification spécifié. Avec une analyse des moyennes à deux facteurs contrôlés, évaluez d'abord les effets d'interaction. Si les effets d'interaction sont statistiquement significatifs, vous ne pouvez pas interpréter les effets principaux sans en tenir compte.
Utilisez les limites de décision comme suit pour tester les hypothèses relatives aux effets d'interaction :- Si un ou plusieurs effets se trouvent en dehors des limites de décision, vous pouvez en conclure que l'effet d'interaction entre les deux facteurs est statistiquement significatif. L'examen des points se trouvant hors des limites de décision peut vous aider à interpréter l'interaction.
- Si aucun effet n'est en dehors des limites de décision, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure qu'il existe un effet d'interaction.
- Graphique des effets principaux
-
Utilisez le graphique des effets principaux pour tester l'hypothèse nulle selon laquelle la moyenne de la population pour chaque niveau de facteur est égale à la moyenne de la population globale au seuil de signification spécifié. Minitab affiche un graphique des effets principaux pour chaque facteur.
Le graphique des effets principaux affiche la mesure moyenne pour chaque niveau de facteur. La ligne centrale représente la moyenne globale de tous les échantillons. Les limites de décision sont calculées à partir de vos données et du seuil de signification spécifié. Utilisez ces limites pour tester les hypothèses relatives aux effets principaux, en suivant les indications ci-dessous :- Si une moyenne d'échantillon se trouve en dehors des limites de décision, vous pouvez rejeter l'hypothèse nulle et en conclure que la différence entre la moyenne du groupe et la moyenne globale est statistiquement significative.
- Si une moyenne d'échantillon est comprise dans les limites de décision, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que la moyenne du groupe est différente de la moyenne globale.
Si tous les niveaux de facteur ont le même nombre d'observations, les limites de décision sont des lignes droites. Si les niveaux n'ont pas tous le même nombre d'observations, les limites de décision diffèrent selon les niveaux.
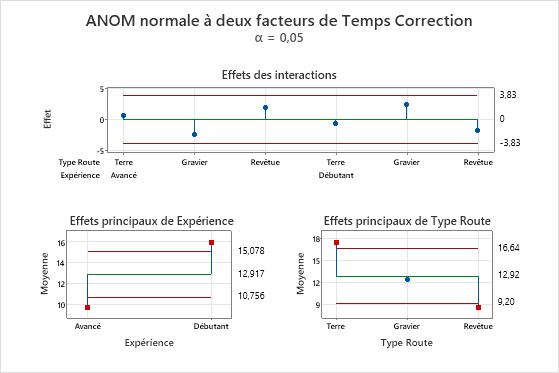
Résultats principaux : graphique des effets principaux, diagramme des effets d'interaction
Dans ce graphique, les effets d'interaction se trouvent largement à l'intérieur des limites de décision, ce qui indique qu'ils ne sont pas statistiquement significatifs. Vous devez ensuite évaluer les effets principaux. Les deux graphiques ci-dessous indiquent les moyennes pour les niveaux des deux facteurs. L'effet principal est la différence entre la moyenne et la ligne centrale.
Dans le graphique des effets principaux pour l'expérience, les points qui représentent les moyennes des niveaux de facteur se trouvent en dehors des limites de décision, tant pour le niveau débutant que pour le niveau avancé. Cela indique que la différence entre chacune de ces moyennes et la moyenne globale est statistiquement significative. Vous pouvez en conclure que le temps de correction moyen est significativement plus bas pour les conducteurs avancés et significativement plus élevé pour les conducteurs débutants.
De même, dans le graphique des effets principaux pour le type de route, les effets principaux pour les routes goudronnées et les routes de terre sont en dehors des limites de décision, ce qui indique que ces effets principaux sont statistiquement significatifs. En revanche, l'effet principal des routes en gravier n'est pas statistiquement significatif.
Carte d'analyse des moyennes pour des données binomiales
La carte d'analyse des moyennes pour données binomiales permet de détecter les proportions anormalement faibles ou élevées.
- Si une proportion d'échantillon se trouve en dehors des limites de décision, vous pouvez rejeter l'hypothèse nulle et en conclure que la différence entre la proportion du groupe et la proportion globale est statistiquement significative.
- Si une proportion d'échantillon est comprise dans les limites de décision, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que la proportion du groupe est différente de la proportion globale.
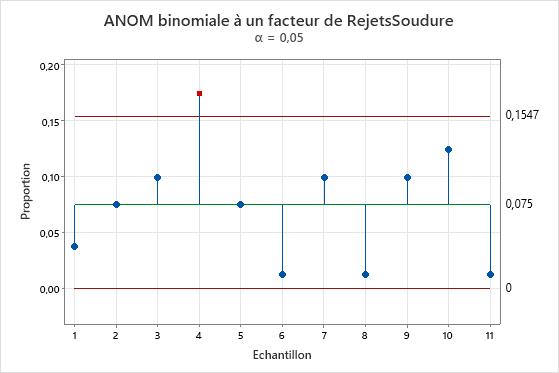
Résultat principal : diagramme d'ANOM binomiale à un facteur
Dans ce diagramme, la proportion de soudures défectueuses dans l'échantillon 4 dépasse la limite de décision. La différence entre la proportion de soudures défectueuses dans ce groupe et la proportion globale est statistiquement significative.
Carte d'analyse des moyennes pour les données de Poisson
La carte d'analyse des moyennes pour données de Poisson permet de détecter les taux d'occurrence anormalement faibles ou élevés.
- Si un taux d'occurrence se trouve en dehors des limites de décision, vous pouvez rejeter l'hypothèse nulle et en conclure que la différence entre le taux d'occurrence du groupe et le taux global est statistiquement significative.
- Si une moyenne d'échantillon est comprise dans les limites de décision, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que le taux d'occurrence du groupe est différent du taux d'occurrence global.
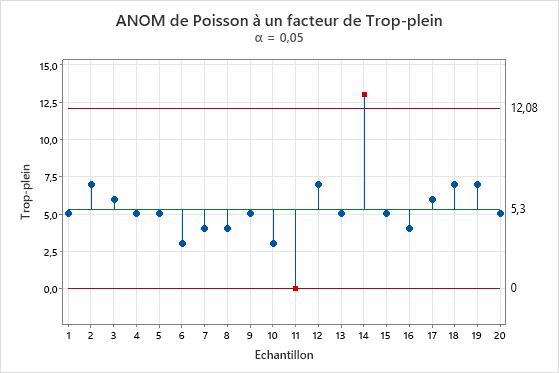
Résultat principal : diagramme d'ANOM de Poisson à un facteur
Dans ce graphique, le nombre de trop-pleins de la 11e machine est 0, ce qui est anormalement faible. La 14e machine a un total de 13 trop-pleins, ce qui est anormalement élevé. Le responsable demande un diagnostic de la 14e machine pour écarter tout problème mécanique.
