Tous les rapports sur la capabilité du procédé pour Rapport sur le procédé

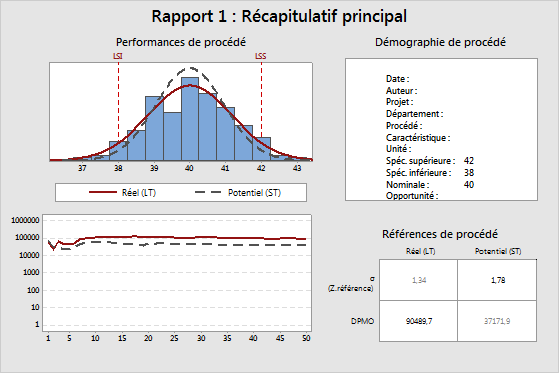
Graphique supérieur Performances de procédé : performances de procédé statiques LT/ST

Les courbes normales dans l'histogramme indiquent la distribution estimée des mesures des valeurs critiques pour la qualité du projet. Les valeurs critiques pour la qualité font référence aux principales caractéristiques mesurables d'un produit ou d'un procédé dont les standards de performances doivent être respectés afin que le client soit satisfait. Les valeurs critiques pour la qualité peuvent comprendre toute variable relative au produit ou au service, ainsi que les limites de spécification supérieure et inférieure.

Minitab calcule ces courbes à partir des estimations à long terme (LT) et à court terme (ST) de la moyenne du procédé et de l'écart type du procédé, puis trace une courbe normale LT et une courbe normale ST. Minitab trace ensuite une courbe normale LT et une courbe normale ST. Dans pratiquement tous les cas, la courbe normale LT est plus ample que la courbe normale ST.

Les limites de spécification (LSI et LSS) fournissent des points de référence. La valeur cible (valeur nominale) est généralement, mais pas toujours, centrée entre les limites de spécification inférieure et supérieure. Dans l'idéal, la moyenne doit être proche de la valeur cible. Dans l'exemple ci-dessus, la moyenne du procédé semble très proche de la valeur cible.

Graphique inférieur Performances de procédé : performances de procédé dynamiques LT/ST

Ce graphique affiche une estimation de la valeur DPMO (défauts pour un million d'opportunités) cumulée après chaque sous-groupe de données pour les graphiques LT (long terme) et ST (court terme). Minitab calcule la valeur DPMO en obtenant d'abord une valeur Z.référence après chaque sous-groupe, puis en la convertissant en une valeur DPMO. Les valeurs Z.référence sont des fonctions de la moyenne estimée et de l'écart type, pour LT et ST.

Si le procédé est stable, les lignes de ce diagramme approchent une valeur constante. Si les lignes ne se stabilisent pas, le procédé n'est pas stable ou il n'y a pas assez de données. Dans l'exemple ci-dessus, les deux lignes ont tendance à fluctuer sur le côté gauche du diagramme, mais elles se stabilisent sur le côté droit. Si les lignes étaient relativement planes sur le côté gauche du diagramme, pour ensuite augmenter ou diminuer de manière constante, cela indiquerait que quelque chose a changé dans le procédé, par exemple, que la moyenne s'est décalée ou que la variation a changé. Dans pratiquement tous les cas, la ligne LT se situe au-dessus de la ligne ST, car le Z.référence LT est inférieur au Z.référence ST, en raison de l'influence du décalage et du glissement du procédé.

Les deux lignes de ce diagramme doivent osciller verticalement sur le côté gauche, où il existe peu de sous-groupes, mais doivent se stabiliser sur le côté droit si les données collectées sont suffisantes et si le procédé est stable. Si les lignes ne se stabilisent pas, les diagrammes du Rapport 4, Statistiques cumulées, doivent vous permettre de déterminer si le problème est dû à une insuffisance de données ou à une instabilité du procédé.

Démographie de procédé

Le tableau des données démographiques regroupe des informations de projet et de procédé que vous spécifiez.

Références de procédé

Les nombres en gras sont les valeurs sigma ST (ou Z.référence) et DPMO LT. La plupart des Black Belts utilisent ces deux valeurs dans les rapports sur les performances.

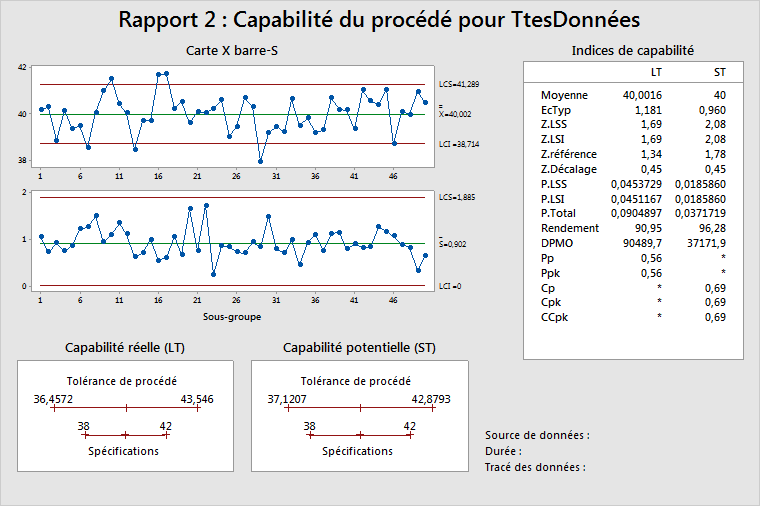
Cartes de contrôle des données de procédé

Affiche la stabilité du procédé au moment de la collecte des données. Pour les sous-groupes dont l'effectif est supérieur à 1, utilisez une carte X barre afin de déterminer la stabilité de la moyenne du procédé et une carte S pour déterminer la stabilité de l'écart type. Si l'effectif des sous-groupes est égal à 1, Minitab affiche une carte I et une carte EM.

Graphiques des capabilités LT/ST

Affiche la tolérance de procédé estimée par rapport aux limites de spécification. La tolérance de procédé correspond au point de centrage du procédé ± 3 écarts types. Il existe deux graphiques car le point de centrage et l'écart type du procédé sont différents pour LT et ST. LT utilise la moyenne du procédé comme point de centrage, tandis que ST utilise la cible (ou le point central entre les spécifications, ou la moyenne du procédé lorsque seulement une spécification est indiquée) comme point de centrage. Pour plus d'informations, reportez-vous à Procédure Minitab relative au choix des valeurs de centrage pour les statistiques à court terme pour Rapport sur le procédé.

En d'autres termes, ces graphiques indiquent si un véhicule (procédé) peut aller dans un garage (spécifications) ou, même, s'il est destiné à ce garage. Dans l'exemple ci-dessus, le procédé est plus étendu que les spécifications. Toutefois, le procédé est centré, comme illustré sur le graphique LT, ce qui indique que le point de centrage du procédé (moyenne) est presque le même que la cible.

Indices de capabilité LT/ST

Affiche les statistiques couramment utilisées pour l'élaboration des rapports sur les performances du procédé. Reportez-vous à Présentation des mesures de capabilité pour consulter une comparaison des statistiques mesurant les performances à long terme (LT) et à court terme (ST).

Utilisez les valeurs de Z.référence pour décrire les performances du procédé. Les statistiques de Z.référence sont fondées sur les conditions de procédé adaptées, mais aboutissent directement à des estimations de la probabilité d'un défaut ou d'une valeur PPM, DPMO ou autre. Les statistiques CCpk et Ppk sont des alternatives possibles, car elles reposent sur les mêmes conditions de procédé que les statistiques de Z.référence.

Pour plus d'informations sur des calculs spécifiques, reportez-vous à Calculs des valeurs de capabilité et des statistiques de procédé pour Rapport sur le procédé.

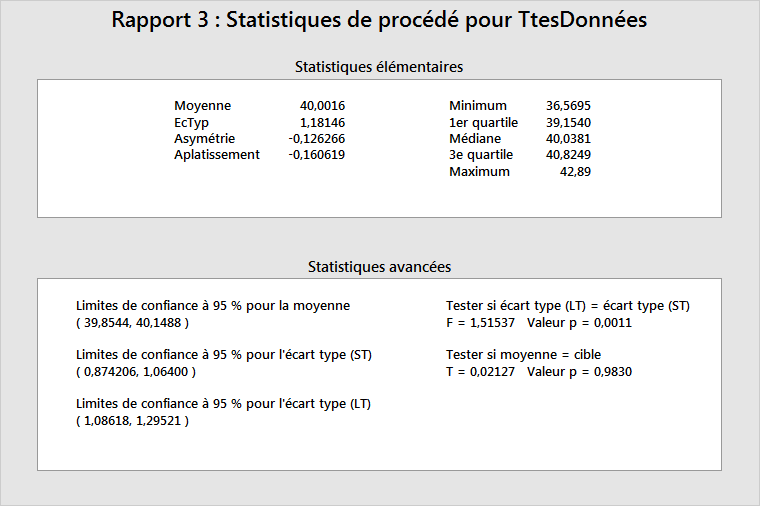
Statistiques élémentaires

Ce tableau indique la moyenne et l'écart type du procédé (moyenne LT et écart type LT), ainsi que d'autres statistiques de base.

L'asymétrie et l'applatissement permettent de déterminer si les données sont distributées normalement. Toutefois, les diagrammes de probabilité sont bien plus utiles. (Dans le rapport 6, la droite de Henry estime la probabilité d'un défaut.)

Les minimum, 1er quartile, médiane, 3e quartile et maximum indiquent la dispersion des données. Par exemple, 25 % des données ne sont pas supérieures à 39,154 (1er quartile), 50 % des données ne sont pas supérieures à 40,0381 (médiane) et 75 % des données ne sont pas supérieures à 40,8249 (3e quartile).

Statistiques avancées

Ce tableau fournit des inférences statistiques pour les paramètres de procédé, la moyenne ST et l'écart type.

La moyenne de procédé comprend un intervalle de confiance à 95 % et des statistiques de test qui montrent si elle est égale à la cible du procédé. Si la moyenne et la cible du procédé ne présentent pas de différence statistiquement significative, la valeur de p doit être > 0,05 et la cible de procédé se trouvera à l'intérieur des bornes de l'intervalle de confiance. Dans l'exemple ci-dessus, le test possède une valeur de p de 0,983 et la cible (40) est à l'intérieur des bornes de l'intervalle de confiance à 95 % pour la moyenne. Vous ne pouvez pas rejeter l'hypothèse nulle selon laquelle la moyenne de procédé est égale à la cible de procédé.

La tableau fournit également des intervalles de confiance à 95 % pour les écarts types LT et ST, ainsi qu'un test pour déterminer si ces deux quantités sont égales. S'il n'existe pas de différence statistiquement significative entre les écarts types de procédé LT et ST, vous pouvez conclure que le procédé ne révèle pas de décalage et/ou de glissement significatif, et qu'il n'existait pas de causes spéciales au moment de la collecte des données. Dans l'exemple ci-dessus, le test de l'égalité des variances possède une valeur de p de 0,0011. Par conséquent, vous devez rejeter l'hypothèse nulle et en conclure que les écarts types LT et ST sont significativement différents.

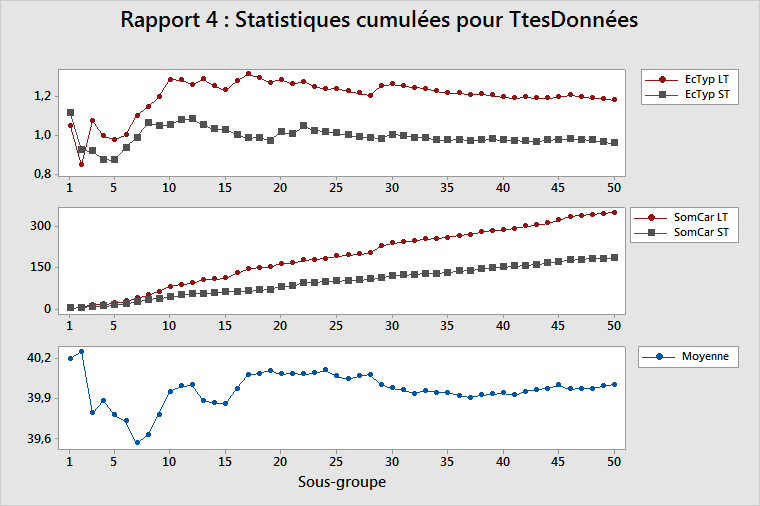
EcTyp LT/ST cumulé

Ce diagramme affiche les estimations de l'écart type LT et de l'écart type ST après chaque sous-groupe de données. Etant donné que toutes les mesures des performances du procédé sont basées sur des estimations de l'écart type du procédé, vous devez déterminer si ces estimations sont adaptées. Leur justesse suppose un procédé stable (dont la variabilité inhérente n'évolue pas) et suffisamment de données pour caractériser ce procédé de manière adéquate.

Les estimations de l'écart type LT et de l'écart type ST doivent osciller considérablement vers le côté gauche du diagramme, où il existe peu de sous-groupes. Si le procédé est stable et que vous avez collecté suffisamment de données, les estimations se stabiliseront sur le côté droit du diagramme. Si les lignes du diagramme continuent d'osciller, cela signifie que vous n'avez pas collecté suffisamment de données ou que la variation du procédé est instable.

Pour qu'un procédé soit stable, il faut que l'écart entre l'écart type LT et l'écart type ST devienne relativement constant. Si le procédé évolue, par exemple à la suite d'un décalage de la moyenne ou d'une modification de la variation, l'écart entre l'écart type LT et l'écart type ST change.

Pour plus d'informations, reportez-vous aux rubriques Identification des décalages de la moyenne de procédé avec Rapport sur le procédé et Identification d'une augmentation de la variabilité du procédé avec Rapport sur le procédé.

SomCar LT/ST cumulée

Ce diagramme affiche la somme des écarts quadratiques (somme totale des carrés ou somme des carrés LT) après chaque sous-groupe de données, et la somme de tous les écarts quadratiques au sein de chaque sous-groupe (somme des carrés "à l'intérieur" ou somme des carrés ST) après chaque sous-groupe de données. Pour plus d'informations, reportez-vous à la rubrique Calculs des sommes des carrés pour Rapport sur le procédé.

La fonctionnalité de somme des carrés ST met à votre disposition un très bon outil de diagnostic pour la détection des changements de la variation inhérente d'un procédé. Si la variation inhérente est stable, la somme des carrés "à l'intérieur" pour chaque sous-groupe varie très peu. Par conséquent, la somme des carrés ST doit augmenter à peu près de la même quantité pour chaque sous-groupe, avec pour résultat une ligne de somme des carrés ST présentant une pente ascendante constante. Toute évolution de la variabilité inhérente du procédé se traduit par une modification de la pente de la ligne de la somme des carrés ST.

La somme des carrés totale est la somme des carrés "à l'intérieur" et la somme des carrés "entre". Par conséquent, la somme des carrés totale est tributaire de la stabilité de la variance du procédé et la moyenne de ce dernier. Si les deux paramètres sont stables, la contribution à la somme des carrés totale sera environ identique pour chaque sous-groupe. Ainsi, la somme des carrés LT doit augmenter environ de la même quantité pour chaque sous-groupe, avec pour résultat une ligne de somme des carrés LT présentant une pente ascendante constante. Toute évolution de la variabilité inhérente du procédé se traduit par une modification de la pente de la ligne de la somme des carrés LT.

Tout changement soudain de la variabilité inhérente du procédé affecte la somme des carrés "à l'intérieur" et la somme des carrés "entre" et, par conséquent, modifie les pentes des lignes de la somme des carrés ST et de la somme des carrés LT. Ainsi, une modification de la pente des deux lignes indique une évolution de la variabilité inhérente du procédé.

Tout décalage de la moyenne du procédé affecte la somme des carrés "entre", mais pas celle des carrés "à l'intérieur" et, par conséquent, modifie la pente de la ligne de somme des carrés LT mais pas celle de la ligne de somme des carrés ST. Ainsi, une modification de la pente de la ligne de la somme des carrés LT sans changement de celle de la ligne de la somme des carrés ST indique un décalage de la moyenne du procédé.

Pour plus d'informations, reportez-vous aux rubriques Identification des décalages de la moyenne de procédé avec Rapport sur le procédé et Identification d'une augmentation de la variabilité du procédé avec Rapport sur le procédé.

Moyenne cumulée

Ce diagramme affiche l'estimation de la moyenne du procédé après chaque sous-groupe. L'ajustement de l'estimation de la moyenne du procédé dépend de la quantité de données collectées et de la stabilité du procédé.

Les estimations doivent considérablement osciller verticalement sur le côté gauche du diagramme, où il existe peu de sous-groupes. Si le procédé est stable et que vous avez collecté suffisamment de données, les estimations doivent se stabiliser sur le côté droit du diagramme. Si les lignes du diagramme continuent d'osciller, cela signifie que vous n'avez pas collecté suffisamment de données ou que la moyenne du procédé subit un glissement sensible. Observez le diagramme EcTyp cumulé pour déterminer si le problème est dû à une quantité de données insuffisante. Si vous ne disposez pas d'assez de données, les lignes LT et ST oscilleront également.

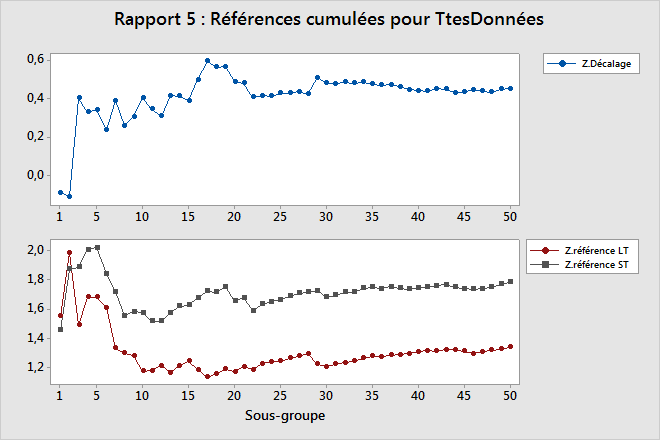
Z.Décalage

Z.Décalage est égal à l'écart entre Z.référence LT et Z.référence ST.

La ligne de ce diagramme doit osciller verticalement sur le gauche côté, où il existe peu de sous-groupes, mais doit se stabiliser sur le côté droit si les données collectées sont suffisantes et si le procédé est stable.

Z.référence LT et Z.référence ST

Le diagramme du Z.référence indique si vous avez collecté suffisamment de données afin de pouvoir utiliser ces statistiques en toute confiance pour créer des rapports sur les performances du procédé. Les deux lignes de ce diagramme doivent osciller verticalement sur le gauche côté, où il existe peu de sous-groupes, mais doivent se stabiliser sur le côté droit si les données collectées sont suffisantes et si le procédé est stable. Si les lignes ne se stabilisent pas, les diagrammes du rapport Statistiques cumulées peuvent vous permettre de déterminer si le problème est dû à une insuffisance de données ou à une instabilité du procédé.

L'écart dans le diagramme du Z.référence et la ligne dans le diagramme du Z.décalage doivent approcher une valeur constante, comme dans l'exemple ci-dessus.

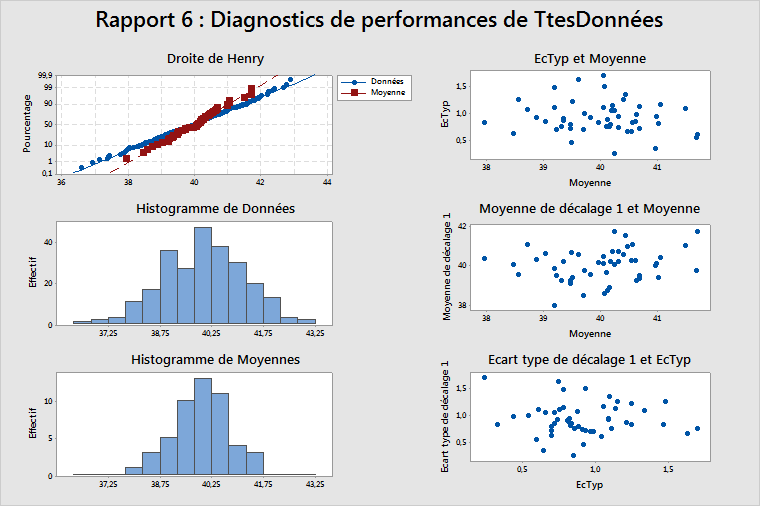
Droite de Henry, histogramme des données et histogramme des moyennes

Ces diagrammes vous aident à déterminer la normalité de vos données. Si vos données sont non normales, les estimations de la probabilité d'un défaut (telles que DPMO) ne seront pas précises. Dans la plupart des cas, ces estimations ont tendance à être inférieures aux valeurs réelles. Par conséquent, avant d'utiliser toute estimation telle que la valeur DPMO, observez la droite de Henry et les deux histogrammes pour déterminer si les données sont au moins relativement normales. Les données de l'exemple ci-dessus semblent être distribuées normalement.

Si les données semblent très asymétriques, essayez d'appliquer une transformation, telle que la transformation de Box-Cox, pour résoudre le problème. Lorsque vous sélectionnez Utiliser la transformation par puissance de Box-Cox (W=Y^λ) avec dans la sous-boîte de dialogue Rapport sur le procédé Options, Minitab transforme automatiquement les données, la cible et les limites de spécification. Toutefois, si vous transformez les données manuellement, vous devez faire de même pour la cible et les limites de spécification.

Ecart type en fonction de la moyenne

En l'absence de corrélation entre les moyennes de sous-groupes et les écarts types de sous-groupes, ce diagramme doit afficher des points dispersés aléatoirement, comme dans l'exemple ci-dessus.

S'il existe une corrélation positive entre les moyennes et les écarts types, les écarts types de sous-groupes ont tendance à augmenter lorsque les moyennes de sous-groupes s'accroissent. La transformation de Box-Cox (λ = 0) est une transformation connue pour la stabilisation de la variance et qui fonctionne généralement bien dans ces cas.

Moyenne de décalage 1 en fonction de la moyenne

Le diagramme de la moyenne de décalage 1 en fonction de la moyenne est un diagramme de (la moyenne du sous-groupe)_i en fonction de (la moyenne du sous-groupe)_i–1. Ce diagramme doit afficher des points dispersés aléatoirement, comme dans l'exemple ci-dessus, ce qui indique l'absence de corrélation entre les moyennes de sous-groupes successifs.

S'il existe une corrélation positive et une moyenne de sous-groupe supérieure à la moyenne de procédé globale, la moyenne du sous-groupe suivant est également susceptible d'être supérieure à la moyenne de procédé globale. Par conséquent, une corrélation positive implique que la moyenne du procédé peut subir un glissement. Si la corrélation est négative, cela indique des moyennes de sous-groupe (inférieures, puis supérieures, puis inférieures) en alternance, et non deux moyennes de sous-groupes inférieures consécutives. Cette corrélation négative indique un contrôle exagéré du procédé.

Ecart type de décalage 1 en fonction de l'écart type

Le diagramme de l'écart type de décalage 1 en fonction de l'écart type est un diagramme de (l'écart type du sous-groupe)_i en fonction de (l'écart type du sous-groupe)_i-1. Ce diagramme doit afficher des points dispersés aléatoirement, comme dans l'exemple ci-dessus, afin de ne présenter aucune corrélation entre les écarts types de sous-groupes successifs.

Comme pour les moyennes de sous-groupes, s'il existe une corrélation positive et que l'écart type d'un sous-groupe est supérieur à l'écart type moyen de tous les sous-groupes, l'écart type du sous-groupe suivant est également fort susceptible d'être supérieur à l'écart type moyen de tous les sous-groupes. Par conséquent, les écarts types de sous-groupes ont tendance à augmenter ou à diminuer. Parallèlement, peuvent apparaître des moyennes qui augmentent ou diminuent, ainsi qu'une corrélation entre les moyennes de sous-groupes et les écarts types de sous-groupes. Dans ce cas, essayez d'utiliser une transformation de Box-Cox avec λ = 0.

L'autocorrélation positive dans les écarts types de sous-groupes peut être causée par l'usure de l'outil ou par une autre dégradation du procédé (avec pour résultat une variation sans cesse croissante) ou par la présence d'un facteur de nuisance non maîtrisé (tel que l'humidité relative) qui a une incidence sur la variation.