Un ingénieur qualité souhaite évaluer la durée de vie d'une ampoule fabriquée par une entreprise. L'ingénieur collecte un échantillon aléatoire de 100 ampoules et note les temps de fonctionnement avant défaillance. Il souhaite calculer la borne de tolérance inférieure (c'est-à-dire le temps de fonctionnement qu'au moins 95 % de toutes les ampoules dépassent).
- Ouvrez le fichier de données échantillons, TempsFonctionnementAmpoule.MWX.
- Sélectionnez .
- Dans la liste déroulante, sélectionnez Un ou plusieurs échantillons, chacun dans une colonne et saisissez Heures.
- Cliquez sur Options.
- Dans Intervalle de tolérance, sélectionnez Borne inférieure.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
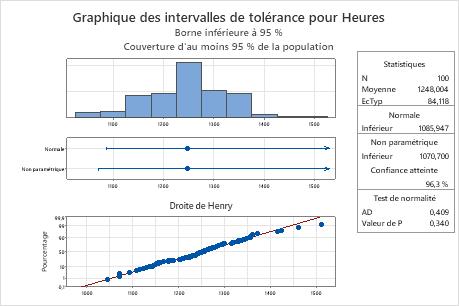
La droite de Henry montre que les points relevés forment approximativement une ligne droite, ce qui indique que les données suivent une loi normale. De plus, la valeur de p est de 0,340 pour le test de normalité, ce qui est supérieur au seuil de signification (α = 0,05). Vous n'êtes donc pas en mesure de conclure que les données ne suivent pas une loi normale. L'ingénieur peut utiliser les résultats de la méthode normale.
La borne inférieure normale étant de 1085,947, l'ingénieur est certain à 95 % qu'au moins 95 % des ampoules auront une durée de vie supérieure à 1086 heures. Pour toutes les ampoules, la durée de vie moyenne est d'environ 1248 heures et l'écart type est d'environ 84,1.
Méthode
| Niveau de confiance | 95 % |
|---|---|
| Pourcentage de population à l'intérieur de l'intervalle | 95 % |
Statistiques
| Variable | N | Moyenne | EcTyp |
|---|---|---|---|
| Heures | 100 | 1248,004 | 84,118 |
Borne de tolérance inférieure à 95 %
| Variable | Méthode normale | Méthode non paramétrique | Confiance atteinte |
|---|---|---|---|
| Heures | 1085,947 | 1070,700 | 96,3% |