Estimations par le maximum de vraisemblance
Les estimations des paramètres par la méthode du maximum de vraisemblance dans la distribution sont calculées par maximisation de la fonction de vraisemblance par rapport aux paramètres. Pour un fichier de données spécifique, les estimations par le maximum de vraisemblance sont les valeurs les plus probables pour les paramètres de distribution.
L'algorithme de Newton-Raphson permet de calculer les estimations des paramètres de distribution par la méthode du maximum de vraisemblance. L'algorithme de Newton-Raphson est une méthode numérique itérative permettant de calculer la valeur maximale d'une fonction. 1
Remarque
Minitab calcule les estimations des paramètres à l'aide de la méthode du maximum de vraisemblance pour toutes les lois à l'exception de la loi log-normale. Pour la loi log-normale, Minitab calcule des estimations de paramètres non biaisées. .
Lois de probabilité
Loi log-normale
 |
|
| CDF |
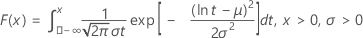 |
| Moyenne |
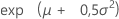 |
| Ecart type |
 |
| Terme | Description |
|---|---|
| μ | Paramètre d'échelle |
| σ | Paramètre de forme |
Loi gamma
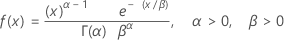 |
|
| CDF |
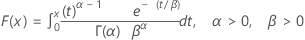 |
| Moyenne | αβ |
| Ecart type | αβ2 |
| Terme | Description |
|---|---|
| α | Paramètre de forme |
| β | Paramètre d'échelle |
Loi exponentielle
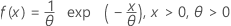 |
|
| CDF |
 |
| Moyenne | θ |
| Ecart type | θ |
| Terme | Description |
|---|---|
| θ | Paramètre d'échelle |
Loi des plus petites valeurs extrêmes
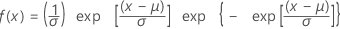 |
|
| CDF |
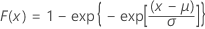 |
| Moyenne |
 |
| Ecart type |
 |
| Terme | Description |
|---|---|
| μ | Paramètre d'emplacement |
| σ | Paramètre d'échelle |
| γ | Constante de Euler (à peu près égale à 0,5772) |
Loi de Weibull
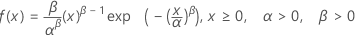 |
|
| CDF |
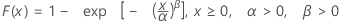 |
| Moyenne |
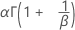 |
| Ecart type |
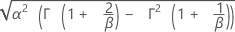 |
| Terme | Description |
|---|---|
| α | Paramètre d'échelle |
| β | Paramètre de forme |
Loi avec valeur extrême la plus grande
 |
|
| CDF |
 |
| Moyenne |
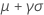 |
| Ecart type |
 |
| Terme | Description |
|---|---|
| μ | Paramètre d'emplacement |
| σ | Paramètre d'échelle |
| γ | Constante de Euler (à peu près égale à 0,5772) |
Loi de distribution logistique
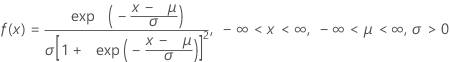 |
|
| CDF |
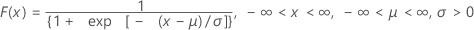 |
| Moyenne | μ |
| Ecart type |
 |
| Terme | Description |
|---|---|
| μ | Paramètre d'emplacement |
| σ | Paramètre d'échelle |
Loi log-logistique
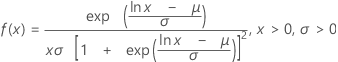 |
|
| CDF |
 |
| Moyenne |
 |
| Ecart type |
 |
| Terme | Description |
|---|---|
| μ | Paramètre d'emplacement |
| σ | Paramètre d'échelle |
