Résultats principaux pour Intervalles de tolérance (loi non normale)

Suivez les étapes ci-dessous pour interpréter des intervalles de tolérance.

Sur ce thème

Etape 1 : Evaluer l'ajustement de la loi de distribution par rapport aux données
Etape 2 : Examiner l'intervalle de tolérance à partir de la méthode appropriée

Etape 1 : Evaluer l'ajustement de la loi de distribution par rapport aux données

Minitab fournit les intervalles de tolérance pour une méthode qui utilise une loi de distribution et une méthode non paramétrique. Si vous pouvez considérer sans risque que vos données suivent la loi de distribution, vous pouvez utiliser l'intervalle de tolérance pour la méthode qui utilise la loi. Si vous ne pouvez pas considérer sans risque que vos données suivent la loi de distribution, vous devez en essayer une autre ou utiliser l'intervalle de tolérance pour la méthode non paramétrique.

Pour déterminer si vous pouvez supposer que les données suivent la loi de distribution, comparez la valeur de p du test d'Anderson-Darling au seuil de signification (α). Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort que les données ne suivent pas la loi de distribution.

Valeur de p ≤ α : les données ne suivent pas la loi (Rejeter H₀): Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure que vos données ne suivent pas la loi de distribution. Dans ce cas, vous devez en essayer une autre ou utiliser l'intervalle de tolérance pour la méthode non paramétrique.
Valeur de p > α : vous ne disposez pas des preuves suffisantes pour conclure que les données ne suivent pas la loi de distribution (Impossible de rejeter H₀): Si la valeur de p est supérieure au seuil de signification, vous ne disposez pas des preuves suffisantes pour conclure que les données ne suivent pas la loi de distribution. Dans ce cas, vous pouvez utiliser l'intervalle de tolérance pour la méthode qui utilise la loi.

Résultats principaux : diagramme de probabilité et valeur de p

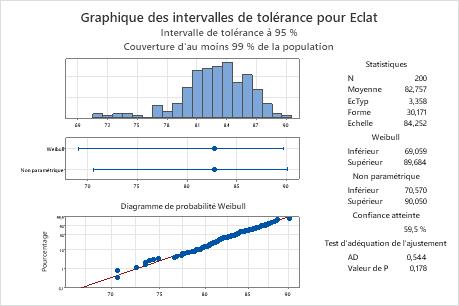
Le diagramme de probabilité indique que les points relevés suivent la droite d'ajustement à la loi de Weibull, ce qui indique que les données suivent une loi de Weibull. De plus, la valeur de p du test d'adéquation de l'ajustement est de 0,178, ce qui est supérieur au seuil de signification de 0,05. Comme vous ne pouvez pas conclure que les données ne suivent pas la loi de Weibull, vous pouvez utiliser l'intervalle pour la loi de Weibull.

Etape 2 : Examiner l'intervalle de tolérance à partir de la méthode appropriée

Minitab fournit les intervalles de tolérance pour la méthode qui utilise la loi de distribution et la méthode non paramétrique qui ne présente aucune loi spécifique. Vous pouvez créer un intervalle de tolérance bilatéral ou un intervalle de tolérance unilatéral qui fournit une borne supérieure ou inférieure.

Bilatéral

Utilisez un intervalle bilatéral pour déterminer les deux valeurs entre lesquelles un certain pourcentage minimal des mesures de population est compris.

Statistiques

Variable	N	Moyenne	EcTyp
Eclat	200	82,757	3,358

Intervalle de tolérance à 95 %

Variable	Méthode Weibull	Méthode non paramétrique	Confiance atteinte
Eclat	(69,059; 89,684)	(70,570; 90,050)	59,54%

Résultats principaux : intervalle de tolérance de 95 %

L'intervalle de Weibull est compris entre environ 69,1 et 89,7 ; le fabriquant peut donc être sûr à 95 % qu'au moins 99 % de l'ensemble des lots de pâte à papier seront compris dans cet intervalle. Pour tous les lots de pâte à papier, le niveau de luminosité moyen est environ de 82,8.

Borne supérieure

Utilisez une borne supérieure pour déterminer la limite dépassant un certain pourcentage minimal des mesures de population.

Borne de tolérance supérieure à 95 %

Variable	Méthode Weibull	Méthode non paramétrique	Confiance atteinte
Eclat	89,131	90,050	86,60%

Résultats principaux : borne de tolérance supérieure de 95 %

Dans cet exemple, la borne supérieure de Weibull est 89,131, vous pouvez donc être certain à 95 % que 99 % de tous les lots de pâte à papier présenteront des mesures d'éclat inférieures ou égales à 89,131. Si vous ne pouvez pas considérer que les données suivent une loi de Weibull, cherchez une loi de distribution adaptée ou prenez en compte la borne supérieure non paramétrique de 90,50. Pour la méthode non paramétrique, la confiance atteinte est de 86,60 %, ce qui est bien inférieur à la valeur cible de 95 %. Ce résultat indique que l'effectif d'échantillon est trop petit pour que la méthode non paramétrique soit exacte.

Borne inférieure

Utilisez une borne inférieure pour déterminer la limite qui est inférieure à un certain pourcentage minimal des mesures de population.

Borne de tolérance inférieure à 95 %

Variable	Méthode Weibull	Méthode non paramétrique	Confiance atteinte
Eclat	71,105	70,570	86,60%

Résultats principaux : borne de tolérance inférieure de 95 %

Dans cet exemple, la borne inférieure de Weibull est 71,105, vous pouvez donc être certain à 95 % que 99 % de tous les lots de pâte à papier présenteront des mesures d'éclat supérieures ou égales à 71,105. Si vous ne pouvez pas considérer que les données suivent une loi de Weibull, cherchez une loi de distribution adaptée ou prenez en compte la borne inférieure non paramétrique de 70,570. Pour la méthode non paramétrique, la confiance atteinte est de 86,60 %, ce qui est bien inférieur à la valeur cible de 95 %. Ce résultat indique que l'effectif d'échantillon est trop petit pour que la méthode non paramétrique soit exacte.