Sur ce thème
Méthode de répartition paramétrique
Les intervalles de tolérance représentent une étendue de valeurs correspondant à la caractéristique de qualité précise d'un produit, susceptible de couvrir un pourcentage minimal spécifique des résultats actuels ou futurs du produit. Utilisez la méthode pour une répartition paramétrique si vous pouvez considérer sans risque que votre échantillon provient d'une population qui suit cette répartition.
Si vos données suivent une répartition paramétrique, une méthode qui l'utilise est plus précise et économique que la méthode non paramétrique. Une méthode qui utilise un loi de distribution obtient des marges d'erreur plus petites avec moins d'observations, à condition que la loi choisie soit adaptée à vos données.
Les méthodes qui utilisent une répartition paramétrique ne sont pas adaptées en cas d'écart important par rapport à cette répartition. Si vous n'êtes pas certain de la répartition de la population, utilisez Identification de loi individuelle - Généralités. Si vous savez que la répartition de la population n'est pas sur la liste pour les intervalles de tolérance non normaux, utilisez la méthode non paramétrique.
Interprétation
- Bilatéral
- Utilisez un intervalle bilatéral pour déterminer les deux valeurs entre lesquelles un certain pourcentage minimal des mesures de population est compris.
- Borne supérieure
- Utilisez une borne supérieure pour déterminer la limite dépassant un certain pourcentage minimal des mesures de population.
- Borne inférieure
- Utilisez une borne inférieure pour déterminer la limite qui est inférieure à un certain pourcentage minimal des mesures de population.
Méthode non paramétrique
Les intervalles de tolérance représentent une étendue de valeurs correspondant à la caractéristique de qualité précise d'un produit, susceptible de couvrir un pourcentage minimal spécifique des résultats actuels ou futurs du produit. Si vous ne pouvez pas considérer sans risque que votre échantillon provient d'une répartition paramétrique présente dans Minitab, vous devez utiliser l'intervalle de tolérance de la méthode non paramétrique.
La méthode non paramétrique exige seulement que les données soient continues. Toutefois, la méthode non paramétrique exige d'importants effectifs d'échantillon pour garantir l'exactitude des résultats. Si l'effectif d'échantillon est trop petit, l'intervalle non paramétrique ne fournit pas de valeur informative et s'étend de l'infini négatif à l'infini positif. Dans ce cas, Minitab affiche un intervalle fini basé sur l'étendue de vos données. Par conséquent, le niveau de confiance obtenu est nettement inférieur au niveau de confiance cible.
Interprétation
- Bilatéral
- Utilisez un intervalle bilatéral pour déterminer les deux valeurs entre lesquelles un certain pourcentage minimal des mesures de population est compris.
- Borne supérieure
- Utilisez une borne supérieure pour déterminer la limite dépassant un certain pourcentage minimal des mesures de population.
- Borne inférieure
- Utilisez une borne inférieure pour déterminer la limite qui est inférieure à un certain pourcentage minimal des mesures de population.
Confiance atteinte
Pour la méthode non paramétrique, Minitab calcule le niveau de confiance atteint. Il s'agit du niveau de confiance exact obtenu à partir de votre échantillon. Il sera généralement supérieur ou égal au niveau de confiance cible, sauf si l'effectif d'échantillon est trop faible.
Si l'effectif d'échantillon est trop petit, l'intervalle non paramétrique ne fournit pas de valeur informative et s'étend de l'infini négatif à l'infini positif. Dans ce cas, Minitab affiche un intervalle fini basé sur l'étendue des données. Par conséquent, le niveau de confiance obtenu est nettement inférieur au niveau de confiance cible.
Interprétation
- Bilatéral
- Utilisez un intervalle bilatéral pour déterminer les deux valeurs entre lesquelles un certain pourcentage minimal des mesures de population est compris.
- Borne supérieure
- Utilisez une borne supérieure pour déterminer la limite dépassant un certain pourcentage minimal des mesures de population.
- Borne inférieure
- Utilisez une borne inférieure pour déterminer la limite qui est inférieure à un certain pourcentage minimal des mesures de population.
Graphique d'intervalle de tolérance
- Histogramme : présente la distribution de vos données échantillons. Chaque barre de l'histogramme représente la fréquence des données dans un intervalle.
- Graphiques d'intervalle : présente la moyenne et les bornes supérieure et/ou inférieure de l'intervalle de tolérance pour chaque méthode. Une ligne verticale à la fin de l'intervalle représente une borne et une flèche désigne l'absence de borne pour ce côté de l'intervalle.
- Diagramme de probabilité : présente l'adéquation des données dans la loi de distribution. Si vos données suivent la loi de distribution, les points de données sur le diagramme de probabilité s'alignent le long de la droite d'ajustement de distribution supposée.
- Tableau statistique : affiche l'effectif de l'échantillon, la moyenne et l'écart type.
- Tableau de répartition paramétrique : présente les bornes supérieure et/ou inférieure de la méthode qui utilise une répartition paramétrique.
- Tableau non paramétrique : affiche les bornes supérieure et/ou inférieure de l'intervalle de tolérance pour la méthode non paramétrique, ainsi que le niveau de confiance obtenu.
- Tableau du test d'adéquation de l'ajustement : présente la valeur de p et la valeur du test d'Anderson-Darling. Pour déterminer si vous pouvez supposer que les données suivent la loi de distribution, comparez la valeur de p du test au seuil de signification (α). Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez conclure que vos données ne suivent pas la loi de distribution. Dans ce cas, essayez d'utiliser une autre loi de distribution ou utilisez l'intervalle de tolérance de la méthode non paramétrique si le niveau de confiance obtenu est proche du niveau cible.
Interprétation
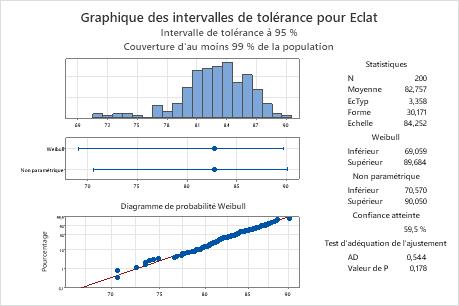
Le diagramme de probabilité indique que les points relevés suivent la droite d'ajustement à la loi de Weibull, ce qui indique que les données suivent une loi de Weibull. De plus, la valeur de p du test d'adéquation de l'ajustement est de 0,178, ce qui est supérieur au seuil de signification de 0,05. Comme vous ne pouvez pas conclure que les données ne suivent pas la loi de Weibull, vous pouvez utiliser l'intervalle pour la loi de Weibull.
L'intervalle de Weibull est compris entre environ 69,1 et 89,7 ; le fabriquant peut donc être sûr à 95 % qu'au moins 99 % de l'ensemble des lots de pâte à papier seront compris dans cet intervalle. Pour tous les lots de pâte à papier, le niveau de luminosité moyen est environ de 82,8.