Un fabricant souhaite évaluer la variabilité du procédé de blanchiment de papier. Le fabricant collecte aléatoirement 200 échantillons de pâte à papier et enregistre le niveau de brillance. Il souhaite calculer une étendue devant comprendre la brillance d'au moins 99 % des lots de pâte à papier.
- Ouvrez le fichier de données échantillons, EclatPâte.MWX.
- Sélectionnez .
- Dans la zone Variables, saisissez Eclat.
- Dans la zone Pourcentage minimal de la population dans l'intervalle, saisissez 99.
- Cliquez sur OK.
Interprétation des résultats
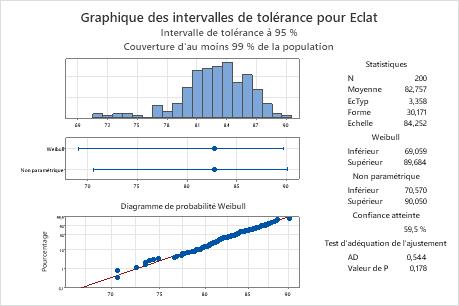
Le diagramme de probabilité indique que les points relevés suivent la droite d'ajustement à la loi de Weibull, ce qui indique que les données suivent une loi de Weibull. De plus, la valeur de p du test d'adéquation de l'ajustement est de 0,178, ce qui est supérieur au seuil de signification de 0,05. Comme vous ne pouvez pas conclure que les données ne suivent pas la loi de Weibull, vous pouvez utiliser l'intervalle pour la loi de Weibull.
L'intervalle de Weibull est compris entre environ 69,1 et 89,7 ; le fabriquant peut donc être sûr à 95 % qu'au moins 99 % de l'ensemble des lots de pâte à papier seront compris dans cet intervalle. Pour tous les lots de pâte à papier, le niveau de luminosité moyen est environ de 82,8.
Méthode
| Loi de distribution | Weibull |
|---|---|
| Niveau de confiance | 95 % |
| Pourcentage de population à l'intérieur de l'intervalle | 99 % |
Statistiques
| Variable | N | Moyenne | EcTyp |
|---|---|---|---|
| Eclat | 200 | 82,757 | 3,358 |
Paramètres de distribution
| Variable | Forme | Echelle |
|---|---|---|
| Eclat | 30,171 | 84,252 |
Intervalle de tolérance à 95 %
| Variable | Méthode Weibull | Méthode non paramétrique | Confiance atteinte |
|---|---|---|---|
| Eclat | (69,059; 89,684) | (70,570; 90,050) | 59,54% |