Sur ce thème
Carte d'essais
Une carte d'essais représente vos données de procédé dans leur ordre de collecte. Elle permet de rechercher des schémas ou des tendances dans vos données, indiquant la présence d'une variation due à des causes spéciales.
Interprétation
La présence de schémas dans les données indique que la variation est due à des causes qui doivent être étudiées et corrigées. La variation due à des causes communes, en revanche, est une variation inhérente au procédé ou faisant naturellement partie de ce dernier. Si seules des causes ordinaires de variation existent dans votre procédé, les données ont un comportement aléatoire.
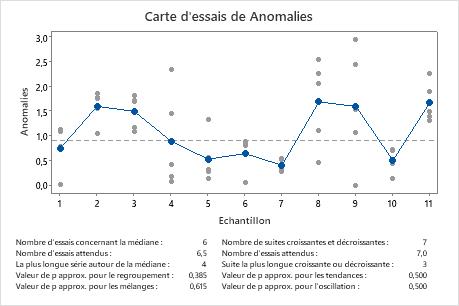
Nombre de suites relatives à la médiane
Le nombre de suites relatives à la médiane est le nombre total de suites au-dessus de la médiane et le nombre total de suites en dessous de celle-ci.
Une suite relative à la médiane est un ensemble d'un ou plusieurs points consécutifs situés du même côté de la ligne centrale. Une suite se termine lorsque la ligne qui relie les points traverse la ligne centrale. Une nouvelle suite commence au point suivant.
Interprétation
- La suite 1 inclut le point 1.
- La suite 2 inclut les points 2 et 3.
- La suite 3 inclut les points 4, 5, 6 et 7.
- La suite 4 inclut les points 8 et 9.
- La suite 5 inclut le point 10.
- La suite 6 inclut le point 11.

Nombre attendu de suites relatives à la médiane
Le nombre attendu de suites relatives à la médiane est le nombre de suites que vous pouvez vous attendre à obtenir dans vos données si celles-ci sont distribuées de façon aléatoire.
Interprétation
Comparez le nombre de suites attendu au nombre de suites réel. Un nombre de suites plus grand qu'attendu peut indiquer que les données proviennent de deux populations (mélanges). Un nombre de suites plus petit qu'attendu peut indiquer un regroupement de données. Utilisez les valeurs de p pour tester la signification statistique de ces comportements.

Plus longue suite relative à la médiane
Nombre de points dans la plus longue suite au-dessus ou en dessous de la médiane. Un point qui se trouve sur la ligne centrale appartient à la suite en dessous de la médiane.
Interprétation

Valeur de p approximative pour le regroupement
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Utilisez la valeur de p pour déterminer si les données sont distribuées de façon aléatoire. L'hypothèse nulle stipule que les données sont distribuées de façon aléatoire.
Interprétation
Une valeur de p inférieure au seuil de signification spécifié indique une tendance au regroupement. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'il existe un schéma non aléatoire dans les données.
- Valeur de p ≤ α : les différences de moyenne sont significativement différentes (rejetez H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle. Vous pouvez conclure que les données ne sont pas distribuées de façon aléatoire.
- Valeur de p > α : les différences de moyenne ne sont pas significativement différentes (impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que les données présentent des schémas non aléatoires. Toutefois, vous ne pouvez pas non plus conclure que les données sont distribuées de façon aléatoire.

Valeur de p approximative pour les mélanges
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Utilisez la valeur de p pour déterminer si les données sont distribuées de façon aléatoire. L'hypothèse nulle stipule que les données sont distribuées de façon aléatoire.
Interprétation
Une valeur de p inférieure au seuil de signification spécifié indique une tendance aux mélanges. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'il existe un schéma non aléatoire dans les données.
- Valeur de p ≤ α : les différences de moyenne sont significativement différentes (rejetez H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle. Vous pouvez conclure que les données ne sont pas distribuées de façon aléatoire.
- Valeur de p > α : les différences de moyenne ne sont pas significativement différentes (impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que les données présentent des schémas non aléatoires. Toutefois, vous ne pouvez pas non plus conclure que les données sont distribuées de façon aléatoire.

Nombre de suites croissantes et décroissantes
Le nombre de suites croissantes et décroissantes est le nombre total de suites ascendantes et descendantes dans vos données.
Une suite croissante est une suite de points consécutifs qui vont uniquement vers le haut. Une suite décroissante est une suite de points consécutifs qui vont uniquement vers le bas. Une suite se termine lorsque la direction (vers le haut ou le bas) change. Par exemple, lorsqu'une valeur est plus petite que celle qu'elle précède, une suite croissante commence et continue jusqu'à ce qu'une valeur soit plus grande que celle qui la suit ; une suite décroissante commence alors.
Minitab considère une suite d'observations consécutives de même valeur (plate) comme une suite décroissante.
Interprétation
- Le point 2 marque la fin de la suite 1.
- Le point 5 marque la fin de la suite 2.
- Le point 6 marque la fin de la suite 3.
- Le point 7 marque la fin de la suite 4.
- Le point 8 marque la fin de la suite 5.
- Le point 10 marque la fin de la suite 6.
- Le point 11 marque la fin de la suite 7.

Comment interpréter une suite plate ?
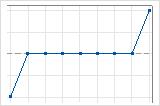
3 suites croissantes et décroissantes
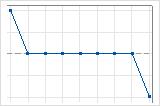
1 suite décroissante
Nombre attendu de suites croissantes et décroissantes
Le nombre attendu de suites croissantes et décroissantes est le nombre de suites que vous pouvez vous attendre à obtenir dans vos données si celles-ci sont distribuées de façon aléatoire.
Interprétation
Comparez le nombre de suites attendu au nombre de suites réel. Un plus grand nombre de suites qu'attendu peut indiquer une oscillation dans les données. Un plus petit nombre de suites qu'attendu peut indiquer une tendance dans les données. Utilisez les valeurs de p pour tester la signification de ces comportements.

Plus longue suite croissante ou décroissante
Nombre de points dans la plus longue suite croissante ou décroissante.
Interprétation

Valeur de p approximative pour les tendances
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Utilisez la valeur de p pour déterminer si les données sont distribuées de façon aléatoire. L'hypothèse nulle stipule que les données sont distribuées de façon aléatoire.
Interprétation
Une valeur de p inférieure au seuil de signification spécifié indique de possibles tendances. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'il existe un schéma non aléatoire dans les données.
- Valeur de p ≤ α : les différences de moyenne sont significativement différentes (rejetez H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle. Vous pouvez conclure que les données ne sont pas distribuées de façon aléatoire.
- Valeur de p > α : les différences de moyenne ne sont pas significativement différentes (impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que les données présentent des schémas non aléatoires. Toutefois, vous ne pouvez pas non plus conclure que les données sont distribuées de façon aléatoire.

Valeur de p approximative pour l'oscillation
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Des probabilités faibles permettent d'invalider l'hypothèse nulle avec plus de certitude.
Utilisez la valeur de p pour déterminer si les données sont distribuées de façon aléatoire. L'hypothèse nulle stipule que les données sont distribuées de façon aléatoire.
Interprétation
Une valeur de p inférieure au seuil de signification spécifié indique une tendance à l'oscillation. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure à tort qu'il existe un schéma non aléatoire dans les données.
- Valeur de p ≤ α : les différences de moyenne sont significativement différentes (rejetez H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle. Vous pouvez conclure que les données ne sont pas distribuées de façon aléatoire.
- Valeur de p > α : les différences de moyenne ne sont pas significativement différentes (impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que les données présentent des schémas non aléatoires. Toutefois, vous ne pouvez pas non plus conclure que les données sont distribuées de façon aléatoire.

