Sur ce thème
Etape 1 : Visualiser l'ajustement de la loi de distribution normale
Les droites de Henry permettent d'évaluer dans quelle mesure les données initiales et transformées suivent la loi normale.
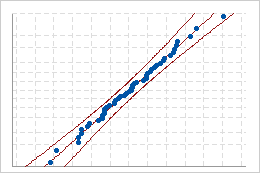
Ajustement correct
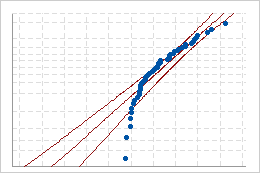
Ajustement incorrect
Remarque
Si les données initiales sont distribuées normalement, Minitab affiche uniquement un diagramme de probabilité simple et n'exécute pas la transformation de Johnson.
Etape 2 : Evaluer l'ajustement de la loi de distribution normale
Utilisez la valeur de p pour déterminer si vous pouvez considérer que les données initiales et transformées suivent la loi normale.
- Une valeur de p inférieure à alpha indique que la loi de distribution normale ne constitue pas un bon ajustement.
- Une valeur de p supérieure ou égale à alpha indique que vous n'êtes pas en mesure d'affirmer que l'ajustement est mauvais. Vous pouvez considérer que les données suivent la loi normale.
Si la transformation de Johnson est efficace, la valeur de p des données transformées est supérieure à alpha.
Important
Soyez prudent lorsque vous interprétez des résultats à partir d'un échantillon très petit ou très grand. En présence d'un très petit échantillon, un test d'adéquation de l'ajustement peut ne pas être assez puissant pour détecter des écarts significatifs par rapport à la loi. En présence d'un très grand échantillon, le test peut être si puissant qu'il détecte même de petits écarts sans signification pratique par rapport à la loi. En plus des valeurs de p, utilisez les diagrammes de probabilité pour évaluer l'ajustement de la loi de distribution.
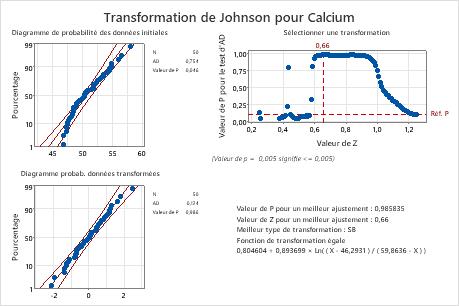
Résultat principal : valeur de p
Dans ces résultats, la valeur de p (0,046) pour les données initiales est inférieure à alpha (0,10), ce qui indique que les données inititiales sur le calcium ne sont pas normales. Pour les données transformées, la valeur de p (0,986) est supérieure à alpha. Vous pouvez donc considérer que les données transformées suivent une loi normale.
Etape 3 : Examiner la fonction de transformation
Minitab affiche les paramètres de la fonction de transformation de Johnson produisant le meilleur ajustement. Minitab utilise cette fonction pour transformer les données initiales.
Par exemple, supposons que la fonction de transformation de Johnson soit égale à 0,762475 + 0,870902 × Ln((X – 46,3174) / (59,677 – X)). Si la valeur des données d'origine pour X est 50, alors la valeur des données transformées pour 50 est calculée comme suit : 0,762475 + 0,870902 × Ln((50 – 46,3174) / (59,677 – 50)), ce qui donne –0,07893.
Remarque
Pour stocker toutes les valeurs de données transformées dans la feuille de travail, indiquez une colonne de stockage lorsque vous effectuez l'analyse.
Pour plus d'informations sur l'algorithme que Minitab utilise pour définir la fonction de transformation de Johnson, reportez-vous à la rubrique Méthodes et formules pour les transformations dans Identification de loi individuelle et cliquez sur "Méthodes et formules pour la transformation de Johnson".
