Sur ce thème
Diagramme de probabilité pour données initiales et transformées
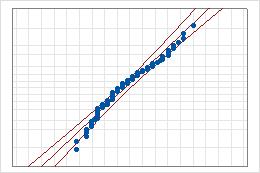
- Ligne centrale
- Percentile attendu de la loi, en fonction des estimations des paramètres par le maximum de vraisemblance.
- Bornes de confiance
- Une ligne courbe placée à gauche indique les bornes inférieures des intervalles de confiance pour les percentiles. Une ligne courbe placée à droite indique les bornes supérieures des intervalles de confiance pour les percentiles.
Interprétation
Les droites de Henry permettent d'évaluer dans quelle mesure les données initiales et transformées suivent la loi normale.
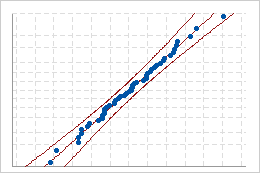
Ajustement correct
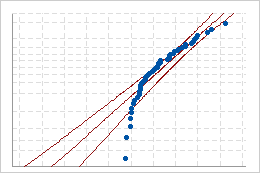
Ajustement incorrect
Remarque
Si les données initiales sont distribuées normalement, Minitab affiche uniquement un diagramme de probabilité simple et n'exécute pas la transformation de Johnson.
N
Nombre de valeurs non manquantes dans l'échantillon. N est le nombre total de valeurs observées.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interprétation
Utilisez N pour évaluer votre effectif d'échantillon.
Important
Soyez prudent lorsque vous interprétez des résultats à partir d'un échantillon très petit ou très grand. En présence d'un très petit échantillon, un test d'adéquation de l'ajustement peut ne pas être assez puissant pour détecter des écarts significatifs par rapport à la loi. En présence d'un très grand échantillon, le test peut être si puissant qu'il détecte même de petits écarts sans signification pratique par rapport à la loi. En plus des valeurs de p, utilisez les diagrammes de probabilité pour évaluer l'ajustement de la loi de distribution.
AD
La statistique d'adéquation de l'ajustement d'Anderson-Darling (AD) mesure les écarts entre la ligne ajustée (selon la loi de distribution sélectionnée) et la fonction en escalier non paramétrique (selon les points de données). La statistique d'Anderson-Darling est une distance quadratique ayant une pondération plus élevée aux extrémités de la loi de distribution.
Interprétation
Minitab utilise la statistique d'Anderson-Darling pour calculer la valeur de p. Cette dernière est une probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle selon laquelle les données suivent la loi de distribution.
En général, des valeurs beaucoup plus petites pour la statistique d'Anderson-Darling indiquent que les données suivent une loi de près. Evitez cependant de comparer directement les valeurs d'AD de différentes lois lorsque ces valeurs sont proches, car les statistiques d'AD sont réparties différemment pour les différentes lois. Pour comparer au mieux l'ajustement de différentes lois, utilisez d'autres critères, tels que les diagrammes de probabilité, les valeurs de p et vos connaissances sur le procédé.
Valeur de p
Pour les valeurs de données initiales et transformées, Minitab fournit une valeur de p pour le test de normalité d'Anderson-Darling (AD). La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Pour un test de normalité d'AD, l'hypothèse nulle est que les données suivent une loi normale. Par conséquent, des valeurs de p faibles tendent à indiquer avec plus de certitude que les données ne suivent pas la loi normale.
Interprétation
Utilisez la valeur de p pour déterminer si les données initiales et transformées suivent la loi normale. Une valeur de p élevée indique un bon ajustement des données.
- Une valeur de p inférieure à alpha indique que la loi de distribution normale ne constitue pas un bon ajustement.
- Une valeur de p supérieure ou égale à alpha indique que vous n'êtes pas en mesure d'affirmer que l'ajustement est mauvais. Vous pouvez considérer que les données suivent la loi normale.
Si la transformation de Johnson est efficace, la valeur de p des données transformées est supérieure à alpha.
Important
Soyez prudent lorsque vous interprétez des résultats à partir d'un échantillon très petit ou très grand. En présence d'un très petit échantillon, un test d'adéquation de l'ajustement peut ne pas être assez puissant pour détecter des écarts significatifs par rapport à la loi. En présence d'un très grand échantillon, le test peut être si puissant qu'il détecte même de petits écarts sans signification pratique par rapport à la loi. En plus des valeurs de p, utilisez les diagrammes de probabilité pour évaluer l'ajustement de la loi de distribution.
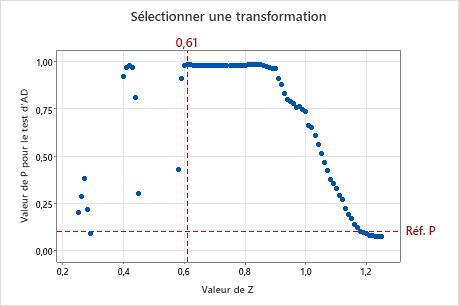
Graphique Sélectionner une transformation
Le graphique Sélectionner une transformation représente la valeur de p du test de normalité d'AD correspondant à chaque valeur de Z des différentes fonctions de transformation de Johnson. Pour déterminer la valeur de Z optimale, la transformation de Johnson utilise une grille de valeurs de Z s'étendant de 0,25 à 1,25 avec un incrément de 0,01, pour un large éventail de lois. Minitab calcule la valeur de p des données transformées pour chaque valeur de Z, puis sélectionne la fonction de transformation ayant la valeur de p la plus élevée par rapport au critère que vous avez indiqué.
Interprétation
Utilisez le graphique Sélectionner une transformation pour voir comment est sélectionnée la fonction de transformation de Johnson en vue d'offrir le meilleur ajustement pour les données. La ligne de référence horizontale indique le critère de valeur de p spécifié pour l'analyse. La ligne de référence verticale indique la valeur de Z de la transformation qui produit le meilleur ajustement. Cette valeur de Z maximale correspond à la valeur de p minimale pour le test de normalité d'AD.
Remarque
Le tableau situé sous le graphique (absent ici) affiche les estimations de paramètres pour la meilleure fonction de transformation. Pour plus d'informations sur l'algorithme que Minitab utilise pour définir la fonction de transformation de Johnson, reportez-vous à la rubrique Méthodes et formules pour les transformations dans Identification de loi individuelle et cliquez sur "Méthodes et formules pour la transformation de Johnson".
Valeur de p pour le meilleur ajustement
La valeur de p pour le meilleur ajustement est celle avec laquelle la fonction de transformation de Johnson offre le meilleur ajustement à la loi normale pour les données transformées. Cette valeur de p, arrondie au millième le plus proche, est également affichée sur le diagramme de probabilité des données transformées.
Pour plus d'informations sur l'interprétation de la valeur de p, reportez-vous à la section relative à la valeur de p.
Pour plus d'informations sur la méthode utilisée par Minitab pour sélectionner la fonction de transformation de Johnson offrant le meilleur ajustement, reportez-vous à la section Graphique Sélectionner une transformation.
Valeur de Z pour le meilleur ajustement
La valeur de Z pour le meilleur ajustement est celle avec laquelle la fonction de transformation de Johnson offre le meilleur ajustement à la loi normale pour les données transformées. La valeur de Z optimale correspond à la valeur de p pour un meilleur ajustement, comme indiqué dans le graphique de la meilleure transformation.
Pour plus d'informations sur la méthode utilisée par Minitab pour sélectionner la fonction de transformation de Johnson offrant le meilleur ajustement à l'aide de la valeur de Z, reportez-vous à la section Graphique Sélectionner une transformation.
Meilleur type de transformation
La transformation de Johnson permet de sélectionner de façon optimale l'une des trois familles de lois : SB, SL, et SU, où B, L et U se rapportent à la variable limitée, log-normale et illimitée, respectivement. Minitab utilise la fonction de la loi sélectionnée pour transformer les données afin qu'elles suivent une loi normale.
Pour plus d'informations sur l'algorithme que Minitab utilise pour définir la fonction de transformation de Johnson, reportez-vous à la rubrique Méthodes et formules pour les transformations dans Identification de loi individuelle et cliquez sur "Méthodes et formules pour la transformation de Johnson".
Fonction de transformation de Johnson
Minitab affiche les paramètres de la fonction de transformation de Johnson produisant le meilleur ajustement. Minitab utilise cette fonction pour transformer les données initiales.
Par exemple, supposons que la fonction de transformation de Johnson soit égale à 0,762475 + 0,870902 × Ln((X – 46,3174) / (59,6770 – X)). Si la valeur des données d'origine pour X est 50, alors la valeur des données transformées pour 50 est calculée comme suit : 0,762475 + 0,870902 × Ln((50 – 46,3174) / (59,6770 – 50)), ce qui donne –0,07893.
Remarque
Pour stocker toutes les valeurs transformées dans la feuille de travail, indiquez une colonne de stockage lorsque vous effectuez l'analyse.
Pour plus d'informations sur l'algorithme que Minitab utilise pour définir la fonction de transformation de Johnson, reportez-vous à la rubrique Méthodes et formules pour les transformations dans Identification de loi individuelle et cliquez sur "Méthodes et formules pour la transformation de Johnson".
