Transformation de Box-Cox
La transformation de Box-Cox estime une valeur lambda, comme indiqué dans le tableau ci-dessous, qui réduit l'écart type d'une variable transformée normalisée. La transformation qui en résulte est Yλ lorsque λ ҂ 0 et ln Y lorsque λ = 0.
La méthode de Box-Cox effectue une recherche dans de nombreux types de transformations. Le tableau suivant présente des transformations courantes dans lesquelles Y' représente la transformation des données Y.
| Valeur lambda (λ) | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
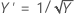 |
 |
 |
Algorithme pour la transformation de Johnson
La transformation de Johnson sélectionne de façon optimale l'une des trois séries de lois pour transformer les données afin qu'elles suivent une loi normale :
| Série de Johnson | Fonction de transformation | Etendue |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , où
Sinh–1(x) = ln [x + racine carrée (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
L'algorithme utilise la procédure suivante :
- Prend en considération la plupart des fonctions de transformation potentielles du système de Johnson.
- Estime les paramètres de la fonction à l'aide de la méthode décrite dans la publication de Chou, et al.1
- Transforme les données avec la fonction de transformation.
- Calcule les statistiques d'Anderson-Darling et la valeur de p correspondante pour les données transformées.
- Sélectionne la fonction de transformation ayant la valeur de p la plus élevée par rapport au critère de valeur de p (la valeur par défaut est 0,10) que vous indiquez dans la boîte de dialogue Transformer. Sinon, aucune transformation n'est adaptée.
Notation
| Terme | Description |
|---|---|
| SB | Distribution de la série de transformations de Johnson avec la variable libérée d'une borne (B) |
| SL | Distribution de la série de transformations de Johnson avec la variable log-normale (L) |
| SU | Distribution de la série de transformations de Johnson avec la variable libérée d'une borne (U) |
Pour plus d'informations sur la transformation de Johnson, reportez-vous à la publication Chou, et al.1 Minitab remplace le test de normalité Shapiro-Wilks utilisé dans ce texte par le test d'Anderson-Darling.
Pour plus d'informations sur le diagramme de probabilité, les percentiles et leurs intervalles de confiance, reportez-vous à la rubrique Méthodes et formules pour les lois de distribution dans Identification de loi individuelle.
