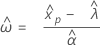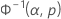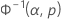Sur ce thème
Diagramme de probabilité
Les diagrammes de probabilité se composent des éléments suivants :
- Des points, qui sont les percentiles estimés des probabilités correspondantes d'un ensemble de données trié.
- Des lignes centrales, qui représentent le percentile attendu de la loi, en fonction des estimations des paramètres par le maximum de vraisemblance. Si la loi est un bon ajustement pour les données, les points s'alignent le long de la ligne centrale.
Probabilités estimées
Minitab estime la probabilité (P) utilisée pour calculer les points du diagramme à l'aide des méthodes suivantes.
- Rang de médiane (méthode de Benard)
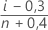
- Rang de moyenne (estimation de Herd-Johnson)

- Kaplan-Meier modifié (Hazen)
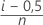
- Estimateur produit-limite de Kaplan-Meier

Notation
| Terme | Description |
|---|---|
| n | Nombre d'observations |
| i | Rang de la ième observation ordonnée x(i), où x(1), x(2), ... x(n) représentent les statistiques d'ordre ou les données rangées par ordre croissant |
Points de diagramme
La ligne centrale du diagramme de probabilité est construite à l'aide des calculs des coordonnées x et y de ce tableau.
| Loi de distribution | Coordonnée x | Coordonnée y |
|---|---|---|
| Plus petite valeur extrême | x | ln(–ln(1 – p)) |
| Plus grande valeur extrême | x | ln(–ln p) |
| Weibull | ln(x) | ln(–ln(1 – p)) |
| Weibull à 3 paramètres | ln(x – seuil) | ln(–ln(1 – p)) |
| Exponentielle | ln(x) | ln(–ln(1 – p)) |
| Exponentielle à 2 paramètres | ln(x – seuil) | ln(–ln(1 – p)) |
| Normale | x | Φ–1normale |
| Log-normale | ln(x) | Φ–1normale |
| Log-normale à 3 paramètres | ln(x – seuil) | Φ–1normale |
| Logistique | x |
 |
| Log-logistique | ln(x) |
 |
| Log-logistique à 3 paramètres | ln(x – seuil) |
 |
| Gamma | x | Φ–1gamma |
| Gamma à 3 paramètres | ln(x – seuil) | Φ–1gamma |
Remarque
Comme les points du diagramme ne dépendent d'aucune loi de distribution, ils sont identiques (avant d'être transformés) pour tout diagramme de probabilité. En revanche, la droite d'ajustement change en fonction de la loi de distribution paramétrique choisie.
Notation
| Terme | Description |
|---|---|
| p | probabilité estimée |
| Φ-1normale | valeur renvoyée pour p par la fonction de répartition inverse de la loi normale standard |
| Φ-1gamma | valeur renvoyée pour p par la fonction de répartition inverse de la loi gamma incomplète |
| ln(x) | logarithme népérien de x |
Percentiles et erreur type de percentiles
Un percentile est une valeur sur une échelle de 100, qui indique le pourcentage de la loi inférieur ou égal à cette valeur. Par défaut, Minitab affiche des tableaux de percentiles pour l'analyse de répartition paramétrique des percentiles courants.
L'erreur type des estimations de percentiles est égale à la racine carrée de la variance.
 ,
,  ,
,  ,
,  ,
,  ,
, 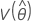 ,
, 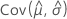 ,
, 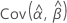 , et
, et 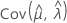 représentent les variances et les covariances des estimations par le maximum de vraisemblance des valeurs μ, σ, α, β, λ et θ extraites de l'élément approprié de l'inverse de la matrice d'informations de Fisher.
représentent les variances et les covariances des estimations par le maximum de vraisemblance des valeurs μ, σ, α, β, λ et θ extraites de l'élément approprié de l'inverse de la matrice d'informations de Fisher.
Les formules utilisées pour les estimations des percentiles et des variances sont les suivantes :
Loi des plus petites valeurs extrêmes
- Percentile
-
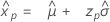
- Variance
-

Loi des plus grandes valeurs extrêmes
- Percentile
-
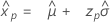
- Variance
-

Loi de Weibull
- Percentile
-

- Variance
-
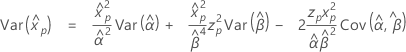
Loi de Weibull à 3 paramètres
- Percentile
-
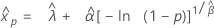
- Variance
-
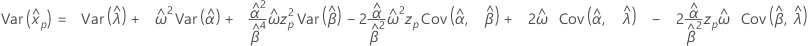
Loi exponentielle
- Percentile
-

- Variance
-

Loi exponentielle à 2 paramètres
- Percentile
-
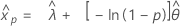
- Variance
-

Loi normale
- Percentile
-
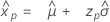
- Variance
-

Loi log-normale
- Percentile
-

- Variance
-

Loi log-normale à 3 paramètres
- Percentile
-

- Variance
-

Loi de distribution logistique
- Percentile
-
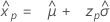
- Variance
-

Loi log-logistique
- Percentile
-

- Variance
-

Loi log-logistique à 3 paramètres
- Percentile
-

- Variance
-

Loi gamma
- Percentile
-
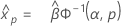
- Variance
-
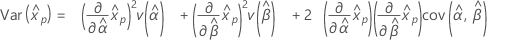
Loi gamma à 3 paramètres
- Percentile
-
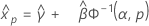
- Variance
-
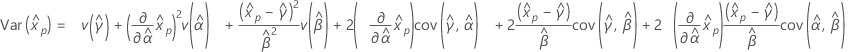
Limites de confiance des percentiles
| Loi de distribution | Limites de confiance |
|---|---|
| Plus petite valeur extrême |
 |
| Plus grande valeur extrême |
 |
| Normale |
 |
| Logistique |
 |
| Weibull |
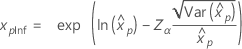 |
| Exponentielle |
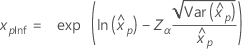 |
| Log-normale |
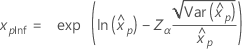 |
| Log-logistique |
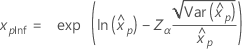 |
| Weibull à 3 paramètres |
Si λ < 0 :
 Si λ ≥ 0 :
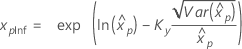 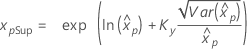 |
| Exponentielle à 2 paramètres |
Si λ < 0 :
 Si λ ≥ 0 :
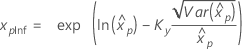 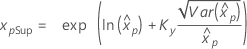 |
| Log-normale à 3 paramètres |
Si λ < 0 :
 Si λ ≥ 0 :
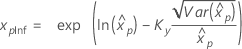 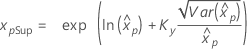 |
| Log-logistique à 3 paramètres |
Si λ < 0 :
 Si λ ≥ 0 :
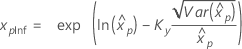 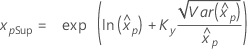 |
Notation
| Terme | Description |
|---|---|
| Kγ | percentile (1 + γ) / 2 d'une loi normale standard |