Sur ce thème
Diagramme de probabilité
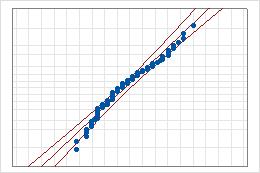
- Ligne centrale
- Percentile attendu de la loi, en fonction des estimations des paramètres par le maximum de vraisemblance.
- Bornes de confiance
- Une ligne courbe placée à gauche indique les bornes inférieures des intervalles de confiance pour les percentiles. Une ligne courbe placée à droite indique les bornes supérieures des intervalles de confiance pour les percentiles.
Interprétation
Utilisez le diagramme de probabilité pour évaluer dans quelle mesure vos données suivent chaque loi.
Si la loi offre un bon ajustement pour les données, les points doivent suivre de près la ligne de distribution ajustée. Si des points s'écartent de la ligne droite, l'ajustement est inacceptable.
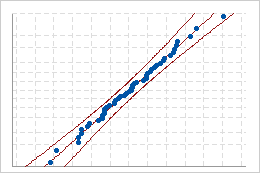
Ajustement correct
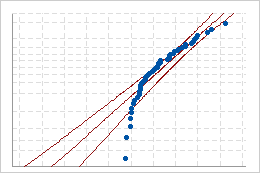
Ajustement incorrect
En plus du diagramme de probabilité, utilisez les mesures d'adéquation de l'ajustement, telles que les valeurs de p d'AD et les valeurs de p LRT pour évaluer l'ajustement de la loi de distribution.
- Choisissez la loi la plus couramment utilisée dans votre secteur industriel ou pour votre application.
- Choisissez la loi qui fournit les résultats les plus prudents. Par exemple, si vous effectuez une analyse de capabilité, vous pouvez utiliser différentes lois, puis choisir celle qui produit les indices de capabilité les plus prudents. Pour plus d'informations, reportez-vous à la rubrique Percentiles de loi pour Identification de loi individuelle et cliquez sur "Pourcentages et percentiles".
- Choisissez la loi la plus simple pami celles qui offrent un bon ajustement à vos données. Par exemple, si une loi à 2 paramètres et une loi à 3 paramètres fournissent un bon ajustement, il est sans doute préférable de choisir la loi à 2 paramètres, plus simple.
AD
La statistique d'adéquation de l'ajustement d'Anderson-Darling (AD) mesure les écarts entre la ligne ajustée (selon la loi de distribution sélectionnée) et la fonction en escalier non paramétrique (selon les points de données). La statistique d'Anderson-Darling est une distance quadratique ayant une pondération plus élevée aux extrémités de la loi de distribution.
Interprétation
Minitab utilise la statistique d'Anderson-Darling pour calculer la valeur de p. Cette dernière est une probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle selon laquelle les données suivent la loi de distribution.
En général, des valeurs beaucoup plus petites pour la statistique d'Anderson-Darling indiquent que les données suivent une loi de près. Evitez cependant de comparer directement les valeurs d'AD de différentes lois lorsque ces valeurs sont proches, car les statistiques d'AD sont réparties différemment pour les différentes lois. Pour comparer au mieux l'ajustement de différentes lois, utilisez d'autres critères, tels que les diagrammes de probabilité, les valeurs de p et vos connaissances sur le procédé.
P
Remarque
Aucune valeur de p n'est disponible pour le test d'AD pour les lois à 3 paramètres, sauf pour la loi de Weibull.
Interprétation
Utilisez la valeur de p pour évaluer l'ajustement de la loi.
- P ≤ α : les données ne suivent pas la loi (rejetez H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous devez rejeter l'hypothèse nulle et en conclure que les données ne suivent pas la loi de distribution.
- P > α : impossible de conclure que les données ne suivent pas la loi (impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que les données ne suivent pas la loi. Vous pouvez considérer que les données suivent la loi.
- Choisissez la loi la plus couramment utilisée dans votre secteur industriel ou pour votre application.
- Choisissez la loi qui fournit les résultats les plus prudents. Par exemple, si vous effectuez une analyse de capabilité, vous utiliser différentes lois, puis choisir celle qui produit les indices de capabilité les plus prudents. Pour plus d'informations, reportez-vous à la rubrique Percentiles de loi pour Identification de loi individuelle et cliquez sur "Pourcentages et percentiles".
- Choisissez la loi la plus simple pami celles qui offrent un bon ajustement à vos données. Par exemple, si une loi à 2 paramètres et une loi à 3 paramètres fournissent un bon ajustement, il est sans doute préférable de choisir la loi à 2 paramètres, plus simple.
Important
Soyez prudent lorsque vous interprétez des résultats à partir d'un échantillon très petit ou très grand. En présence d'un très petit échantillon, un test d'adéquation de l'ajustement peut ne pas être assez puissant pour détecter des écarts significatifs par rapport à la loi. En présence d'un très grand échantillon, le test peut être si puissant qu'il détecte même de petits écarts sans signification pratique par rapport à la loi. En plus des valeurs de p, utilisez les diagrammes de probabilité pour évaluer l'ajustement de la loi de distribution.
Test d'adéquation de l'ajustement
| Loi de distribution | AD | P | Valeur de P LRT |
|---|---|---|---|
| Normale | 0,754 | 0,046 | |
| Transformation de Box-Cox | 0,414 | 0,324 | |
| Log-normale | 0,650 | 0,085 | |
| Log-normale à 3 paramètres | 0,341 | * | 0,017 |
| Exponentielle | 20,614 | <0,003 | |
| Exponentielle 2 paramètres | 1,684 | 0,014 | 0,000 |
| Weibull | 1,442 | <0,010 | |
| Weibull 3 paramètres | 0,230 | >0,500 | 0,000 |
| Plus petite valeur extrême | 1,656 | <0,010 | |
| Plus grande valeur extrême | 0,394 | >0,250 | |
| Gamma | 0,702 | 0,071 | |
| Gamma 3 paramètres | 0,268 | * | 0,006 |
| Logistique | 0,726 | 0,034 | |
| Log-logistique | 0,659 | 0,050 | |
| Log-logistique 3 paramètres | 0,432 | * | 0,027 |
| Transformation de Johnson | 0,124 | 0,986 |
Dans ces résultats, plusieurs lois présentent une valeur de p supérieure à 0,05. La loi de Weibull à 3 paramètres (p > 0,500) et la loi des plus grandes valeurs extrêmes (p > 0,250) sont celles qui ont les valeurs de p les plus grandes et semblent mieux ajustées que les autres aux données échantillons. De plus, la transformation de Box-Cox (p = 0,324) et la transformation de Johnson (p = 0,986) transforment efficacement les données pour qu'elles suivent une loi normale.
Remarque
Pour plusieurs lois de distributions, Minitab affiche également les résultats correspondant à la même loi, mais avec un paramètre supplémentaire. Par exemple, pour la loi log-normale, Minitab affiche les résultats des versions à 2 et 3 paramètres. Pour les lois avec des paramètres en plus, utilisez la valeur de p du test de rapport de vraisemblance (p LRT) pour déterminer si l'ajout du paramètre supplémentaire améliore l'ajustement de la loi de façon significative. Une valeur de p LRT inférieure à 0,05 suggère que l'amélioration de l'ajustement est significative. Pour plus d'informations, reportez-vous à la section sur la valeur de p LRT.
Valeur de P LRT
Pour plusieurs lois de distribution, Minitab affiche également les résultats correspondant à la même loi, mais avec un paramètre supplémentaire. Pour chaque version avec un paramètre supplémentaire d'une loi, Minitab indique la valeur de p pour le test de rapport de vraisemblance (p LRT). Une valeur de p est une probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Pour le test de rapport de vraisemblance utilisé dans l'identification de loi individuelle, l'hypothèse nulle est que les données suivent la loi la plus petite (celle qui a le plus petit nombre de paramètres). Par conséquent, plus les valeurs de p LRT sont faibles, plus vous pouvez être certain que l'ajustement de la loi est significativement amélioré avec un paramètre supplémentaire.
Interprétation
Dans ces cas-là, utilisez la valeur de p LRT pour déterminer si l'ajout du paramètre supplémentaire améliore l'ajustement de façon significative par rapport à la plus petite loi.
- p ≤ α : la loi de distribution la plus grande (celle qui a le plus grand nombre de paramètres) améliore l'ajustement de façon significative (rejetez H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et conclure que l'ajustement de la loi de distribution est significativement amélioré avec l'utilisation d'un paramètre supplémentaire.
- p > α : impossible de conclure que la loi de distribution la plus grande (celle qui a le plus grand nombre de paramètres) améliore l'ajustement de façon significative (impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que l'ajustement de la loi de distribution est significativement amélioré avec l'utilisation d'un paramètre supplémentaire.
La valeur de p LRT est également utile pour les lois à 3 paramètres pour lesquelles aucune méthode n'a été mise en place afin de calculer la valeur de p. Dans ces situations, il est recommandé d'examiner la valeur de p de la loi à 2 paramètres correspondante. Il convient ensuite d'observer la valeur de p LRT de la loi à 3 paramètres, afin de déterminer si la loi à 3 paramètres est significativement meilleure que la loi à 2 paramètres.
Dans ces résultats, les valeurs de p LRT pour la loi log-normale à 3 paramètres (0,017), la loi de Weibull à 3 paramètres (0,000), la loi gamma à 3 paramètres (0,006) et la loi log-logistique à 3 paramètres (0,027) suggèrent que ces lois offrent un ajustement significativement meilleur par rapport aux lois à 2 paramètres correspondantes.
Test d'adéquation de l'ajustement
| Loi de distribution | AD | P | Valeur de P LRT |
|---|---|---|---|
| Normale | 0,754 | 0,046 | |
| Transformation de Box-Cox | 0,414 | 0,324 | |
| Log-normale | 0,650 | 0,085 | |
| Log-normale à 3 paramètres | 0,341 | * | 0,017 |
| Exponentielle | 20,614 | <0,003 | |
| Exponentielle 2 paramètres | 1,684 | 0,014 | 0,000 |
| Weibull | 1,442 | <0,010 | |
| Weibull 3 paramètres | 0,230 | >0,500 | 0,000 |
| Plus petite valeur extrême | 1,656 | <0,010 | |
| Plus grande valeur extrême | 0,394 | >0,250 | |
| Gamma | 0,702 | 0,071 | |
| Gamma 3 paramètres | 0,268 | * | 0,006 |
| Logistique | 0,726 | 0,034 | |
| Log-logistique | 0,659 | 0,050 | |
| Log-logistique 3 paramètres | 0,432 | * | 0,027 |
| Transformation de Johnson | 0,124 | 0,986 |
