N
Nombre de valeurs non manquantes dans l'échantillon. N est le nombre total de valeurs observées.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interprétation
Utilisez N pour évaluer votre effectif d'échantillon.
Important
Soyez prudent lorsque vous interprétez des résultats à partir d'un échantillon très petit ou très grand. En présence d'un très petit échantillon, un test d'adéquation de l'ajustement peut ne pas être assez puissant pour détecter des écarts significatifs par rapport à la loi. En présence d'un très grand échantillon, le test peut être si puissant qu'il détecte même de petits écarts sans signification pratique par rapport à la loi. En plus des valeurs de p, utilisez les diagrammes de probabilité pour évaluer l'ajustement de la loi de distribution.
N*
Nombre de valeurs manquantes dans votre échantillon. N* est le nombre de cellules dans la feuille de travail contenant le symbole de valeur manquante *.
| Total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Moyenne
Elle est calculée comme la moyenne des données, c'est-à-dire la somme de toutes les observations, divisée par le nombre d'observations.
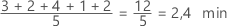
Interprétation
La moyenne permet de décrire l'échantillon avec une seule valeur, qui représente le centre des données. De nombreuses analyses statistiques utilisent la moyenne comme point de référence standard.
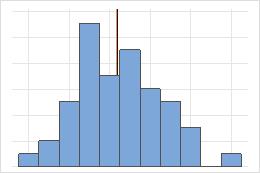
Moyenne et médiane dans une loi symétrique
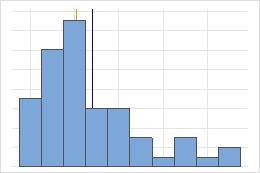
Moyenne et médiane dans une loi non symétrique
Pour la loi symétrique, la moyenne (ligne bleu) et la médiane (ligne orange) sont presque identiques. Par conséquent, les lignes se superposent et il est impossible de les distinguer l'une de l'autre. Pour la loi non symétrique, les données sont asymétriques à droite, et la moyenne est donc supérieure à la médiane.
EcTyp
L'écart type (EcTyp) est la mesure la plus courante de la dispersion ou de la répartition des données autour de la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon.
Interprétation
Utilisez l'écart type pour déterminer la dispersion des données par rapport à la moyenne. Un écart type d'échantillon supérieur indique que vos données sont réparties plus largement autour de la moyenne.
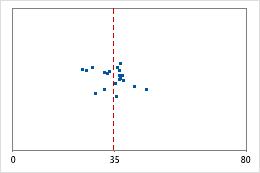
Hôpital 1
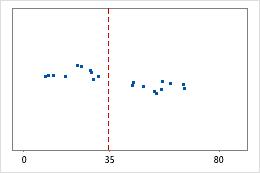
Hôpital 2
Durée jusqu'à la sortie de l'hôpital
Les administrateurs de deux hôpitaux étudient le temps que passent les patients dans le service des urgences de leurs établissements jusqu'à leur sortie. Bien que ces durées moyennes soient pratiquement identiques (35 minutes), les écarts types diffèrent de manière significative. L'écart type pour l'hôpital 1 est d'environ 6. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 6 minutes par rapport à la moyenne (ligne bleue). L'écart type pour l'hôpital 2 est d'environ 20. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 20 minutes par rapport à la moyenne (ligne en pointillés).
Médiane
La médiane représente le milieu de l'ensemble de données. Ce point de milieu est celui qui sépare les observations en deux moitiés égales, l'une supérieure à la valeur, l'autre inférieure. La médiane est déterminée en classant les observations dans l'ordre, puis en prenant l'observation de rang [N + 1] / 2 dans l'ordre obtenu. Si le nombre d'observations est pair, la médiane est la valeur comprise entre les observations classées aux numéros N / 2 et [N / 2] + 1.
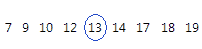
Pour les données ordonnées ci-dessous, la médiane est 13. Autrement dit, la moitié des valeurs est inférieure ou égale à 13 et l'autre est supérieure ou égale à 13.
Interprétation

Moyenne et médiane dans une loi symétrique

Moyenne et médiane dans une loi non symétrique
Pour la loi symétrique, la moyenne (ligne bleu) et la médiane (ligne orange) sont presque identiques. Par conséquent, les lignes se superposent et il est impossible de les distinguer l'une de l'autre. Pour la loi non symétrique, les données sont asymétriques à droite, et la moyenne est donc supérieure à la médiane.
Minimum
Plus petite valeur de données.
Dans ces données, le minimum est de 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le minimum pour détecter une éventuelle valeur aberrante. Si une valeur est inhabituellement basse, recherchez les causes possibles de cette anomalie, par exemple une erreur d'entrée des données ou de mesure.
L'une des manières les plus simples d'estimer la dispersion des données consiste à comparer le minimum et le maximum pour déterminer l'étendue. L'étendue est la différence entre le maximum et le minimum dans l'ensemble de données. Pour évaluer la dispersion des données, examinez aussi d'autres mesures, telles que l'écart type.
Maximum
Plus grande valeur de données.
Dans ces données, le maximum est 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le maximum pour détecter une éventuelle valeur aberrante. Si une valeur est inhabituellement élevée, recherchez les causes possibles de cette anomalie, par exemple une erreur d'entrée des données ou de mesure.
L'une des manières les plus simples d'estimer la dispersion des données consiste à comparer le minimum et le maximum pour déterminer l'étendue. L'étendue est la différence entre le maximum et le minimum dans l'ensemble de données. Pour évaluer la dispersion des données, examinez aussi d'autres mesures, telles que l'écart type.
Asymétrie
L'asymétrie évalue dans quelle mesure vos données ne sont pas symétriques.
Interprétation
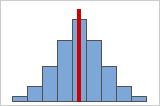
Figure A : Données symétriques, distribuées normalement
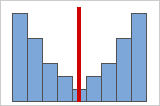
Figure B : Données symétriques, distribuées de façon non normale
Lois symétriques
Plus vos données sont symétriques, plus leur valeur d'asymétrie est proche de 0. La figure A représente des données distribuées normalement, qui présentent par définition une asymétrie relativement faible. La ligne au milieu de l'histogramme de données normales montre que les deux côtés se reflètent l'un l'autre. Toutefois, l'absence d'asymétrie n'implique pas en soi une normalité. La figure B représente une loi de distribution dont les deux côtés se reflètent également, bien que les données ne soient pas distribuées normalement.
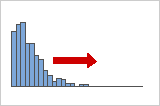
Lois à asymétrie positive ou asymétriques à droite
Les données présentant une asymétrie positive sont également dites asymétriques à droite, car la "queue" de leur loi de distribution pointe vers la droite. Les données présentant une asymétrie positive ont une valeur d'asymétrie supérieure à 0. Les données salariales présentent souvent une asymétrie positive : dans une entreprise, un grand nombre d'employés ont un salaire relativement bas tandis qu'une minorité de personnes touchent un très haut salaire.
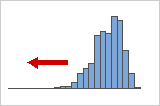
Lois à asymétrie négative ou asymétriques à gauche
Les données présentant une asymétrie négative sont souvent dites asymétriques à gauche, car la "queue" de leur loi de distribution pointe vers la gauche. Les données présentant une asymétrie négative ont une valeur d'asymétrie inférieure à 0. Les données sur les taux de défaillance présentent souvent une asymétrie négative. Par exemple, très peu d'ampoules grillent immédiatement, la plupart cessent de fonctionner longtemps après.
Aplatissement
L'aplatissement indique dans quelle mesure les queues d'une loi diffèrent de la loi normale.
Interprétation
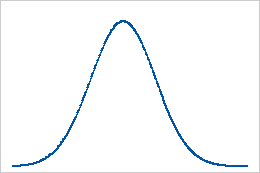
Référence : valeur d'aplatissement de 0
Les données qui suivent parfaitement une loi normale ont une valeur d'aplatissement de 0. Des données distribuées normalement servent de référence pour l'aplatissement. Une valeur d'aplatissement qui s'écarte significativement de 0 peut indiquer que les données ne sont pas distribuées normalement.
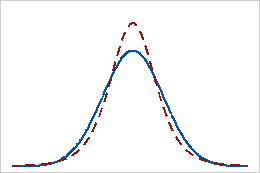
Aplatissement positif
Les données possédant une valeur d'aplatissement positive présentent des queues plus lourdes qu'avec la loi normale. Par exemple, les données qui suivent une loi t ont une valeur d'aplatissement positive. La ligne pleine représente la loi normale et la ligne en pointillés représente une loi t possédant une valeur d'aplatissement positive.
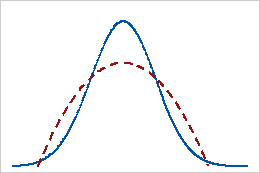
Aplatissement négatif
Les données possédant une valeur d'aplatissement négative présentent des queues plus légères qu'avec la loi normale. Par exemple, les données qui suivent une loi bêta avec un premier et un deuxième paramètres de forme égaux à 2 ont une valeur d'aplatissement négative. La ligne pleine représente la loi normale et la ligne en pointillés représente une loi bêta possédant une valeur d'aplatissement négative.
