Exemple pour la fonction Identification de loi individuelle

Interprétation des résultats

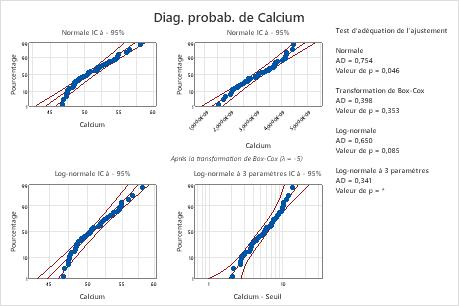
Minitab affiche un diagramme de probabilité et une valeur de p pour chaque loi et chaque transformation. Si une loi représente un bon ajustement pour les données (ou si une transformation est efficace), les points du diagramme suivent une ligne droite et sont compris dans les limites de confiance, tandis que la valeur de p est supérieure au seuil alpha. On utilise souvent un seuil alpha de 0,05. La valeur de p du test de rapport de vraisemblance (LRT) indique si l'ajout d'un paramètre supplémentaire améliore l'ajustement de la loi de façon significative. Une valeur de p LRT inférieure à 0,05 suggère que l'amélioration est significative.

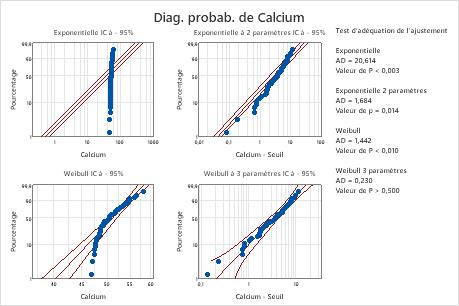
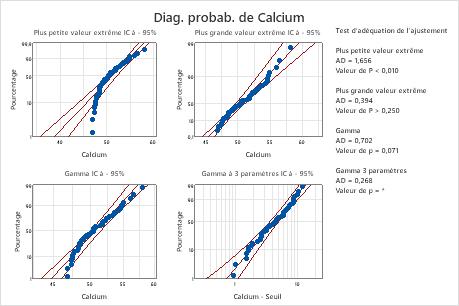
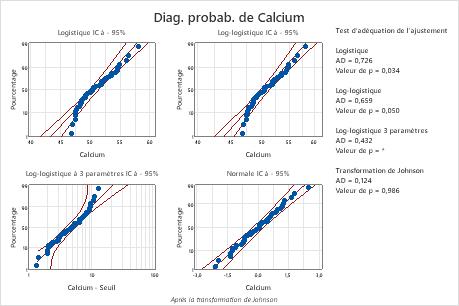
Pour ces données, la loi de Weibull à trois paramètres (p > 0,500) et la loi des plus grandes valeurs extrêmes (p > 0,250) sont adaptées aux données. L'ajout d'un troisième paramètre améliore significativement l'ajustement de la loi log-normale (p LRT = 0,017), de la loi de Weibull (p LRT = 0,000), de la loi gamma (p LRT = 0,006) et de la loi log-logistique (p LRT = 0,027).

La transformation de Box-Cox (p = 0,324) et la transformation de Johnson (p = 0,986) sont efficaces pour ces données. Après la transformation, la loi normale fournit un bon ajustement pour les valeurs transformées.

Statistiques descriptives

N	N*	Moyenne	EcTyp	Médiane	Minimum	Maximum	Asymétrie	Aplatissement
50	0	50,782	2,76477	50,4	46,8	58,1	0,644923	-0,287071

Transformation de Box-Cox : λ = -4

Fonction de transformation de Johnson :

0,804604 + 0,893699 × Ln( ( X - 46,2931 ) / ( 59,8636 - X ) )

Test d'adéquation de l'ajustement

Loi de distribution	AD	P	Valeur de P LRT
Normale	0,754	0,046
Transformation de Box-Cox	0,414	0,324
Log-normale	0,650	0,085
Log-normale à 3 paramètres	0,341	*	0,017
Exponentielle	20,614	<0,003
Exponentielle 2 paramètres	1,684	0,014	0,000
Weibull	1,442	<0,010
Weibull 3 paramètres	0,230	>0,500	0,000
Plus petite valeur extrême	1,656	<0,010
Plus grande valeur extrême	0,394	>0,250
Gamma	0,702	0,071
Gamma 3 paramètres	0,268	*	0,006
Logistique	0,726	0,034
Log-logistique	0,659	0,050
Log-logistique 3 paramètres	0,432	*	0,027
Transformation de Johnson	0,124	0,986

Estimations de MaxV des paramètres de distribution

Loi de distribution	Emplacement	Forme	Echelle	Seuil
Normal*	50,78200		2,76477
Transformation de Box-Cox*	0,00000		0,00000
Log-normale*	3,92612		0,05368
Log-normale à 3 paramètres	1,69295		0,46849	44,74011
Exponentielle			50,78200
Exponentielle 2 paramètres			4,06326	46,71873
Weibull		17,82470	52,13681
Weibull 3 paramètres		1,47605	4,53647	46,66579
Plus petite valeur extrême	52,22257		2,95894
Plus grande valeur extrême	49,50370		2,16992
Gamma		351,04421	0,14466
Gamma 3 paramètres		2,99218	1,63698	45,88376
Logistique	50,57182		1,59483
Log-logistique	3,92259		0,03121
Log-logistique 3 paramètres	1,54860		0,32763	45,46180
Transformation de Johnson*	0,02897		0,97293