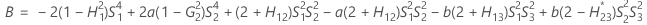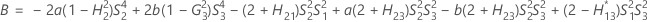Sur ce thème
- Intervalle de confiance pour le rapport de la variance de répétabilité et de la variance totale
- Intervalle de confiance pour le rapport de la variance de reproductibilité et de la variance totale
- Intervalle de confiance pour le rapport de la variance de pièce et de la variance totale
- Intervalle de confiance pour le rapport de la variance d'instrumentation et de la variance totale
Intervalle de confiance pour le rapport de la variance de répétabilité et de la variance totale
Il existe deux modes de calcul possibles. Tout d'abord, Minitab calcule les bornes à l'aide de la méthode des grands échantillons modifiés. En cas de non-respect de certaines conditions pendant les calculs, Minitab utilise l'approximation de Satterthwaite. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Méthode des grands échantillons modifiés


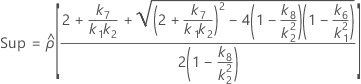
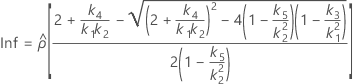
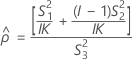
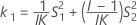
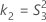
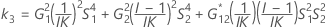
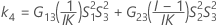

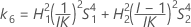
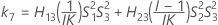

Les deux conditions de l'existence des bornes inférieure et supérieure à l'aide de la méthode des grands échantillons modifiés sont les suivantes :
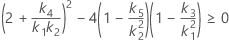
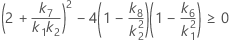
Si les deux conditions ne sont pas réunies, Minitab ne peut pas utiliser cette méthode pour créer les bornes inférieure et supérieure. Minitab utilisera l'approximation de Satterthwaite pour calculer les bornes inférieure et supérieure.
Approximation de Satterthwaite
Les formules des bornes inférieure et supérieure s'appliquent toujours, excepté Inf et Sup, définies comme suit :
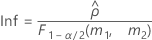

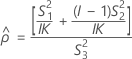
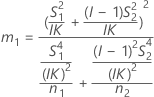
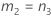
Notation
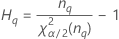
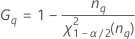
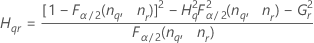
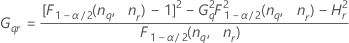
| Terme | Description |
|---|---|
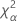 | le α * 100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance pour le rapport de la variance de reproductibilité et de la variance totale
Il existe deux modes de calcul possibles. Tout d'abord, Minitab calcule les bornes à l'aide de la méthode des grands échantillons modifiés. En cas de non-respect de certaines conditions pendant les calculs, Minitab utilise une autre approximation. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Méthode des grands échantillons modifiés
Les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) * 100 % sont calculées par le biais de la résolution d'équations quadratiques.
- Borne inférieure
-

- Borne supérieure
-

Deuxième méthode
Si B2– 4AC < 0, il est impossible de résoudre l'équation quadratique. Dans ce cas, Minitab utilise la deuxième méthode pour estimer les intervalles de confiance. Les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) * 100 % sont calculées comme suit :
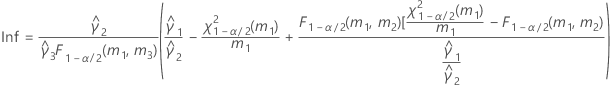
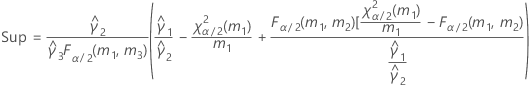
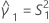
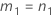
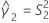
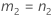

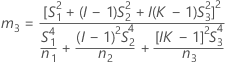
Notation
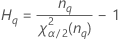
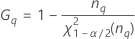
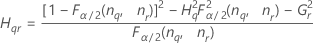
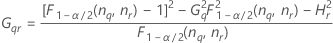
| Terme | Description |
|---|---|
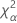 | le α * 100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance pour le rapport de la variance de pièce et de la variance totale
Il existe deux modes de calcul possibles. Tout d'abord, Minitab calcule les bornes à l'aide de la méthode des grands échantillons modifiés. En cas de non-respect de certaines conditions pendant les calculs, Minitab utilise une autre approximation. Remplacez α/2 par α dans H et G pour calculer les bornes de confiance unilatérales.
Méthode des grands échantillons modifiés
- Borne inférieure
-

- Borne supérieure
-

Deuxième méthode
Si B2– 4AC < 0, il est impossible de résoudre l'équation quadratique. Dans ce cas, Minitab utilise la deuxième méthode pour estimer les intervalles de confiance. Les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) * 100 % sont calculées comme suit :
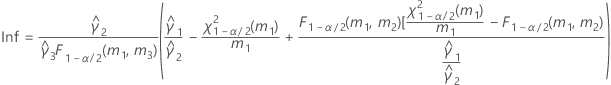
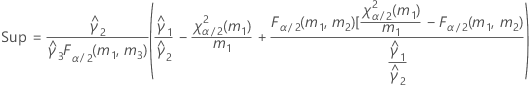

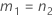

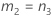

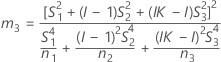
Notation
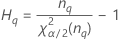
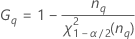
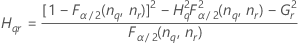
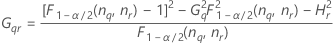
| Terme | Description |
|---|---|
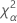 | le α * 100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance pour le rapport de la variance d'instrumentation et de la variance totale
Borne inférieure = 1 – (borne inférieure de l'IC pour le rapport de la variance de pièce et de la variance totale)
Borne supérieure = 1 – (borne supérieure de l'IC pour le rapport de la variance de pièce et de la variance totale)